【题目】已知∠AOC=∠BOD=α(0°<α<180°)
(1)如图1,若α=90°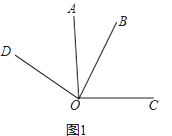
①写出图中一组相等的角(除直角外) , 理由是
②试猜想∠COD和∠AOB在数量上是相等、互余、还是互补的关系,并说明理由;
(2)如图2,∠COD+∠AOB和∠AOC满足的等量关系是;当α=°,∠COD和∠AOB互余.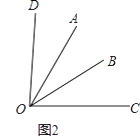
参考答案:
【答案】
(1)AOD=∠BOC,同角的余角相等
(2)互补,45
【解析】解:(1)①∵∠AOC=∠BOD=90°,
∴∠AOD+∠AOB=∠BOC+∠AOB=90°,
∴∠AOD=∠BOC;②∵∠AOD=∠BOD﹣∠AOB=90°﹣∠AOB,
∴∠COD=∠AOD+∠AOC=90°﹣∠AOB+90°,
∴∠AOB+∠COD=180°,
∴∠COD和∠AOB互补;(2)由(1)可知∠COD+∠AOB=∠BOD+∠AOC=α+α=2α,
所以,∠COD+∠AOB=2∠AOC,
若∠COD和∠AOB互余,则2∠AOC=90°,
所以,∠AOC=45°,
即α=45°.
所以答案是:(1)AOD=∠BOC,同角的余角相等;(2)互补,45.
【考点精析】解答此题的关键在于理解余角和补角的特征的相关知识,掌握互余、互补是指两个角的数量关系,与两个角的位置无关.
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算:﹣1+3= .
-
科目: 来源: 题型:
查看答案和解析>>【题目】在矩形ABCD中,E为CD的中点,H为BE上的一点,
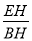 =3,连接CH并延长交AB于点G,连接GE并延长交AD的延长线于点F.
=3,连接CH并延长交AB于点G,连接GE并延长交AD的延长线于点F.(1)求证:
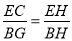 ;
;(2)若∠CGF=90°,求
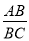 的值.
的值.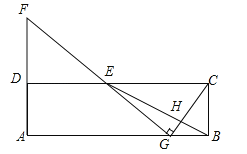
-
科目: 来源: 题型:
查看答案和解析>>【题目】某品牌手机的进价为1200元,按原价的八折出售可获利14%,则该手机的原售价为( )
A.1800元
B.1700元
C.1710元
D.1750元 -
科目: 来源: 题型:
查看答案和解析>>【题目】已知不等式
 的最小整数解为方程
的最小整数解为方程 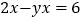 的解,求代数式
的解,求代数式  的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】因式分解:
(1)3a(a﹣2b)+6b(2b﹣a)
(2)(x2+4y2)2﹣16x2y2
-
科目: 来源: 题型:
查看答案和解析>>【题目】如果一个四边形的两条对角线互相平分,互相垂直且相等,那么这个四边形是( )
A. 矩形 B. 菱形 C. 正方形 D. 菱形、矩形或正方形
相关试题

