【题目】在矩形ABCD中,E为CD的中点,H为BE上的一点,![]() =3,连接CH并延长交AB于点G,连接GE并延长交AD的延长线于点F.
=3,连接CH并延长交AB于点G,连接GE并延长交AD的延长线于点F.
(1)求证:![]() ;
;
(2)若∠CGF=90°,求![]() 的值.
的值.
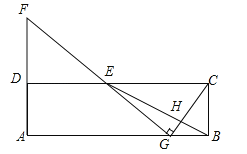
参考答案:
【答案】(1)证明见解析;(2)![]() .
.
【解析】
试题分析:(1)根据相似三角形判定的方法,判断出△CEH∽△GBH,即可推得结论;
(2)作EM⊥AB于M,则EM=BC=AD,AM=DE,设DE=CE=3a,则AB=CD=6a,由(1)得:![]() =3,得出BG=
=3,得出BG=![]() CE=a,AG=5a,证明△DEF∽△GEC,由相似三角形的性质得出EGEF=DEEC,由平行线证出
CE=a,AG=5a,证明△DEF∽△GEC,由相似三角形的性质得出EGEF=DEEC,由平行线证出![]() =
=![]() ,得出EF=
,得出EF=![]() EG,求出EG=
EG,求出EG=![]() a,在Rt△EMG中,GM=2a,由勾股定理求出BC=EM=
a,在Rt△EMG中,GM=2a,由勾股定理求出BC=EM=![]() a,即可得出结果.
a,即可得出结果.
试题解析:(1)证明:∵四边形ABCD是矩形,∴CD∥AB,AD=BC,AB=CD,AD∥BC,∴△CEH∽△GBH,∴![]() .
.
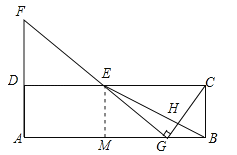
(2)解:作EM⊥AB于M,如图所示:
则EM=BC=AD,AM=DE,∵E为CD的中点,∴DE=CE,设DE=CE=3a,则AB=CD=6a,由(1)得:![]() =3,∴BG=
=3,∴BG=![]() CE=a,∴AG=5a,∵∠EDF=90°=∠CGF,∠DEF=∠GEC,∴△DEF∽△GEC,∴
CE=a,∴AG=5a,∵∠EDF=90°=∠CGF,∠DEF=∠GEC,∴△DEF∽△GEC,∴![]() ,∴EGEF=DEEC,∵CD∥AB,∴
,∴EGEF=DEEC,∵CD∥AB,∴![]() =
=![]() ,∴
,∴![]() =
=![]() ,∴EF=
,∴EF=![]() EG,∴EG
EG,∴EG![]() EG=3a3a,解得:EG=
EG=3a3a,解得:EG=![]() a,在Rt△EMG中,GM=2a,∴EM=
a,在Rt△EMG中,GM=2a,∴EM=![]() =
=![]() a,∴BC=
a,∴BC=![]() a,∴
a,∴![]() =
=![]() =
=![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,已知△ABC三个顶点的坐标分别是A(2,2),B(4,0),C(4,﹣4)
(1)请画出△ABC向左平移6个单位长度后得到的△A1B1C1;
(2)以点O为位似中心,将△ABC缩小为原来的
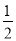 ,得到△A2B2C2,请在y轴右侧画出△A2B2C2,并求出∠A2C2B2的正弦值.
,得到△A2B2C2,请在y轴右侧画出△A2B2C2,并求出∠A2C2B2的正弦值.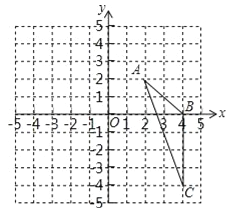
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,在所给正方形网格图中完成下列各题:(用直尺画图,保留痕迹)
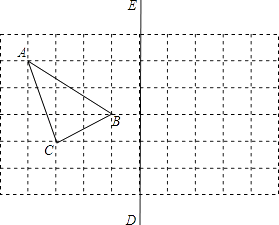
(1)求出格点△ABC(顶点均在格点上)的面积;
(2)画出格点△ABC关于直线DE对称的△A1B1C1;
(3)在DE上画出点Q,使△QAB的周长最小. -
科目: 来源: 题型:
查看答案和解析>>【题目】计算:﹣1+3= .
-
科目: 来源: 题型:
查看答案和解析>>【题目】某品牌手机的进价为1200元,按原价的八折出售可获利14%,则该手机的原售价为( )
A.1800元
B.1700元
C.1710元
D.1750元 -
科目: 来源: 题型:
查看答案和解析>>【题目】已知∠AOC=∠BOD=α(0°<α<180°)
(1)如图1,若α=90°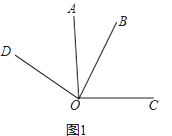
①写出图中一组相等的角(除直角外) , 理由是
②试猜想∠COD和∠AOB在数量上是相等、互余、还是互补的关系,并说明理由;
(2)如图2,∠COD+∠AOB和∠AOC满足的等量关系是;当α=°,∠COD和∠AOB互余.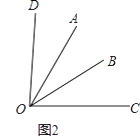
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知不等式
 的最小整数解为方程
的最小整数解为方程 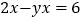 的解,求代数式
的解,求代数式  的值.
的值.
相关试题

