【题目】如图,已知直线![]() 分别交
分别交![]() 轴、
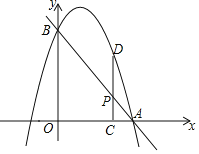
轴、![]() 轴于点A、B,抛物线过A,B两点,点P是线段AB上一动点,过点P作PC
轴于点A、B,抛物线过A,B两点,点P是线段AB上一动点,过点P作PC![]()
![]() 轴于点C,交抛物线于点D.
轴于点C,交抛物线于点D.
(1)若抛物线的解析式为![]() ,设其顶点为M,其对称轴交AB于点N.
,设其顶点为M,其对称轴交AB于点N.
①求点M、N的坐标;
②是否存在点P,使四边形MNPD为菱形?并说明理由;
(2)当点P的横坐标为1时,是否存在这样的抛物线,使得以B、P、D为顶点的三角形与![]() AOB相似?若存在,求出满足条件的抛物线的解析式;若不存在,请说明理由.
AOB相似?若存在,求出满足条件的抛物线的解析式;若不存在,请说明理由.
参考答案:
【答案】(1)①![]()
![]() ②答案见解析 (2)存在,
②答案见解析 (2)存在,![]() 或
或![]()
【解析】
(1)①如图1,把抛物线解析式配成顶点式可得到顶点为![]() 的坐标为
的坐标为![]() ,
,![]() ,然后计算自变量为
,然后计算自变量为![]() 对应的一次函数值可得到
对应的一次函数值可得到![]() 点坐标;
点坐标;
②易得![]() ,设
,设![]() 点坐标为
点坐标为![]() ,则
,则![]() ,则
,则![]() ,由于
,由于![]() ,根据平行四边形的判定方法,当
,根据平行四边形的判定方法,当![]() 时,四边形
时,四边形![]() 为平行四边形,即
为平行四边形,即![]() ,求出
,求出![]() 得到此时
得到此时![]() 点坐标为
点坐标为![]() ,
,![]() ,接着计算出
,接着计算出![]() ,然后比较
,然后比较![]() 与
与![]() 的大小关系可判断平行四边形
的大小关系可判断平行四边形![]() 是否为菱形;
是否为菱形;
(2)如图2,利用勾股定理计算出![]() ,再表示出
,再表示出![]() ,则可计算出
,则可计算出![]() ,接着表示出抛物线解析式为
,接着表示出抛物线解析式为![]() ,则可用
,则可用![]() 表示出点
表示出点![]() 坐标为
坐标为![]() ,所以
,所以![]() ,由于
,由于![]() ,根据相似三角形的判定方法,当
,根据相似三角形的判定方法,当![]() 时,
时,![]() ,即
,即![]() ;当
;当![]() 时,
时,![]() ,即
,即![]() ,然后利用比例性质分别求出
,然后利用比例性质分别求出![]() 的值,从而得到对应的抛物线的解析式.
的值,从而得到对应的抛物线的解析式.
(1)①如图1,
![]() ,
,
![]() 顶点为
顶点为![]() 的坐标为
的坐标为![]() ,
,![]() ,
,
当![]() 时,
时,![]() ,则点
,则点![]() 坐标为
坐标为![]() ,
,![]() ;
;
②不存在.
理由如下:
![]() ,
,
设![]() 点坐标为
点坐标为![]() ,则
,则![]() ,
,
![]() ,
,
![]() ,
,
当![]() 时,四边形
时,四边形![]() 为平行四边形,即
为平行四边形,即![]() ,解得
,解得![]() (舍去),
(舍去),![]() ,此时
,此时![]() 点坐标为
点坐标为![]() ,
,![]() ,
,
![]() ,
,
![]() ,
,
![]() 平行四边形
平行四边形![]() 不为菱形,
不为菱形,
![]() 不存在点
不存在点![]() ,使四边形
,使四边形![]() 为菱形;
为菱形;
(2)存在.
如图2,![]() ,
,![]() ,则
,则![]() ,
,
当![]() 时,
时,![]() ,则
,则![]() ,
,
![]() ,
,
设抛物线的解析式为![]() ,
,
把![]() 代入得
代入得![]() ,解得
,解得![]() ,
,
![]() 抛物线的解析式为
抛物线的解析式为![]() ,
,
当![]() 时,
时,![]() ,则
,则![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() 当
当![]() 时,
时,![]() ,即
,即![]() ,解得
,解得![]() ,此时抛物线解析式为
,此时抛物线解析式为![]() ;
;
当![]() 时,
时,![]() ,即
,即![]() ,解得
,解得![]() ,此时抛物线解析式为
,此时抛物线解析式为![]() ;
;
综上所述,满足条件的抛物线的解析式为![]() 或
或![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AB=7.5,AC=9,S△ABC=
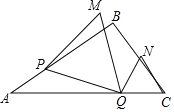
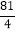 .动点P从A点出发,沿AB方向以每秒5个单位长度的速度向B点匀速运动,动点Q从C点同时出发,以相同的速度沿CA方向向A点匀速运动,当点P运动到B点时,P、Q两点同时停止运动,以PQ为边作正△PQM(P、Q、M按逆时针排序),以QC为边在AC上方作正△QCN,设点P运动时间为t秒.
.动点P从A点出发,沿AB方向以每秒5个单位长度的速度向B点匀速运动,动点Q从C点同时出发,以相同的速度沿CA方向向A点匀速运动,当点P运动到B点时,P、Q两点同时停止运动,以PQ为边作正△PQM(P、Q、M按逆时针排序),以QC为边在AC上方作正△QCN,设点P运动时间为t秒.(1)求cosA的值;
(2)当△PQM与△QCN的面积满足S△PQM=
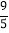 S△QCN时,求t的值;
S△QCN时,求t的值;(3)当t为何值时,△PQM的某个顶点(Q点除外)落在△QCN的边上.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知正方形ABCD,点M是边BA延长线上的动点(不与点A重合),且AM<AB,△CBE由△DAM平移得到.若过点E作EH⊥AC,H为垂足,则有以下结论:①点M位置变化,使得∠DHC=60°时,2BE=DM;②无论点M运动到何处,都有DM=
 HM;③无论点M运动到何处,∠CHM一定大于135°.其中正确结论的序号为_____.
HM;③无论点M运动到何处,∠CHM一定大于135°.其中正确结论的序号为_____.
-
科目: 来源: 题型:
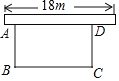
查看答案和解析>>【题目】为响应荆州市“创建全国文明城市”号召,某单位不断美化环境,拟在一块矩形空地上修建绿色植物园,其中一边靠墙,可利用的墙长不超过18m,另外三边由36m长的栅栏围成.设矩形ABCD空地中,垂直于墙的边AB=xm,面积为ym2(如图).
(1)求y与x之间的函数关系式,并写出自变量x的取值范围;
(2)若矩形空地的面积为160m2,求x的值;
(3)若该单位用8600元购买了甲、乙、丙三种绿色植物共400棵(每种植物的单价和每棵栽种的合理用地面积如下表).问丙种植物最多可以购买多少棵?此时,这批植物可以全部栽种到这块空地上吗?请说明理由.
甲
乙
丙
单价(元/棵)
14
16
28
合理用地(m2/棵)
0.4
1
0.4
-
科目: 来源: 题型:
查看答案和解析>>【题目】某校团委计划在元且期间组织优秀团员到敬老院去服务,现选出了10名优秀团员参加服务,其中男生6人,女生4人.
 若从这10人中随机选一人当队长,求选中女生当队长的概率;
若从这10人中随机选一人当队长,求选中女生当队长的概率; 现决定从甲、乙中选一人当队长,他们准备以游戏的方式决定由谁担任,游戏规则如下:将四张牌面数字分别为2,3,4,5的扑克牌洗匀后,数字朝下放于桌面,从中任取2张,若牌面数字之和为偶数,则选甲为队长;否则,选乙为队长
现决定从甲、乙中选一人当队长,他们准备以游戏的方式决定由谁担任,游戏规则如下:将四张牌面数字分别为2,3,4,5的扑克牌洗匀后,数字朝下放于桌面,从中任取2张,若牌面数字之和为偶数,则选甲为队长;否则,选乙为队长 试问这个游戏公平吗?请用树状图或列表法说明理由.
试问这个游戏公平吗?请用树状图或列表法说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】某市政府规定:若本市企业按生产成本价提供产品给大学生销售,则政府给该企业补偿
 补偿额
补偿额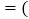 批发价
批发价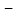 生产成本价
生产成本价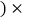 销售量
销售量 大学生小明投资销售本市企业生产的一种新型节能灯,调查发现,每月销售量
大学生小明投资销售本市企业生产的一种新型节能灯,调查发现,每月销售量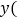 件
件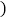 与销售单价
与销售单价 元
元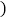 之间的关系近似满足一次函数:
之间的关系近似满足一次函数: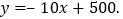 已知这种节能灯批发价为每件12元,设它的生产成本价为每件m元
已知这种节能灯批发价为每件12元,设它的生产成本价为每件m元
(1)当
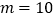 时.
时.①若第一个月的销售单价定为20元,则第一个月政府要给该企业补偿多少元?
②设所获得的利润为
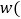 元
元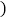 ,当销售单价定为多少元时,每月可获得最大利润?
,当销售单价定为多少元时,每月可获得最大利润?(2)物价部门规定,这种节能灯的销售单价不得超过30元
 今年三月小明获得赢利,此时政府给该企业补偿了920元,若m,x都是正整数,求m的值.
今年三月小明获得赢利,此时政府给该企业补偿了920元,若m,x都是正整数,求m的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在
 中,
中, ,
, ,
, ,点P是射线BA上的一个动点,以BP为半径的
,点P是射线BA上的一个动点,以BP为半径的 交射线BC于点D,直线PD交直线AC于点E,点P关于直线AC的对称点为点
交射线BC于点D,直线PD交直线AC于点E,点P关于直线AC的对称点为点 ,连结
,连结 ,
, ,设直线
,设直线 与直线BC交于点F.
与直线BC交于点F. 当点P在线段BA上时,
当点P在线段BA上时, 求证:
求证: ;
; 连结
连结 ,当
,当 时,求
时,求 的长;
的长; 连结AD,AF,当
连结AD,AF,当 恰为等边三角形时,求此时四边形
恰为等边三角形时,求此时四边形 的面积;
的面积; 当四边形
当四边形 在
在 内部时,请直接写出BP的取值范围.
内部时,请直接写出BP的取值范围.
相关试题

