Question

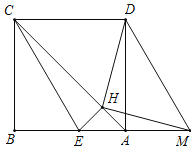
【题目】如图，已知正方形ABCD，点M是边BA延长线上的动点（不与点A重合），且AM＜AB，△CBE由△DAM平移得到．若过点E作EH⊥AC，H为垂足，则有以下结论：①点M位置变化，使得∠DHC=60°时，2BE=DM；②无论点M运动到何处，都有DM=HM；③无论点M运动到何处，∠CHM一定大于135°．其中正确结论的序号为_____．

Answer 1

【答案】①②③

【解析】先判定△MEH≌△DAH（SAS），即可得到△DHM是等腰直角三角形，进而得出DM=HM；依据当∠DHC=60°时，∠ADH=60°﹣45°=15°，即可得到Rt△ADM中，DM=2AM，即可得到DM=2BE；依据点M是边BA延长线上的动点（不与点A重合），且AM＜AB，可得∠AHM＜∠BAC=45°，即可得出∠CHM＞135°．

由题可得，AM=BE，

∴AB=EM=AD，

∵四边形ABCD是正方形，EH⊥AC，

∴EM=AH，∠AHE=90°，∠MEH=∠DAH=45°=∠EAH，

∴EH=AH，

∴△MEH≌△DAH（SAS），

∴∠MHE=∠DHA，MH=DH，

∴∠MHD=∠AHE=90°，△DHM是等腰直角三角形，

∴DM=HM，故②正确；

当∠DHC=60°时，∠ADH=60°﹣45°=15°，

∴∠ADM=45°﹣15°=30°，

∴Rt△ADM中，DM=2AM，

即DM=2BE，故①正确；

∵点M是边BA延长线上的动点（不与点A重合），且AM＜AB，

∴∠AHM＜∠BAC=45°，

∴∠CHM＞135°，故③正确，

故答案为：①②③．