【题目】如图,E,F是四边形ABCD的对角线AC上两点,AF=CE,DF=BE,DF∥BE.
求证: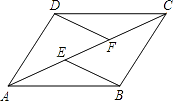
(1)△AFD≌△CEB;
(2)四边形ABCD是平行四边形.
参考答案:
【答案】
(1)解:∵DF∥BE,
∴∠DFE=∠BEF.
∵∠AFD+∠DFE=180°,∠CEB+∠BEF=180°,
∴∠AFD=∠CEB.
又∵AF=CE,DF=BE,
∴△AFD≌△CEB(SAS)
(2)解:由(1)知△AFD≌△CEB,
∴∠DAC=∠BCA,AD=BC,
∴AD∥BC.
∴四边形ABCD是平行四边形(一组对边平行且相等的四边形是平行四边形)
【解析】(1)根据DF∥BE,得到∠DFE=∠BEF,再由等角的补角相等得出∠AFD=∠CEB,然后可证△AFD≌△CEB;(2)由(1)知△AFD≌△CEB,可得∠DAC=∠BCA,AD=BC,所以AD∥BC.根据一组对边平行且相等的四边形是平行四边形可证结论。
【考点精析】本题主要考查了平行线的判定与性质和平行四边形的判定的相关知识点,需要掌握由角的相等或互补(数量关系)的条件,得到两条直线平行(位置关系)这是平行线的判定;由平行线(位置关系)得到有关角相等或互补(数量关系)的结论是平行线的性质;两组对边分别平行的四边形是平行四边形:两组对边分别相等的四边形是平行四边形;一组对边平行且相等的四边形是平行四边形;两组对角分别相等的四边形是平行四边形;对角线互相平分的四边形是平行四边形才能正确解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知一元二次方程(m﹣3)x2+2mx+m+1=0有两个不相等的实数根,并且这两个根又不互为相反数.
(1)求m的取值范围;
(2)当m在取值范围内取最小正偶数时,求方程的根.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列命题中的真命题是( )
A.在所有连接两点的线中直线最短
B.经过两点有且只有一条直线
C.内错角互补则两直线平行
D.空间中,如果一条直线和两条直线中的一条垂直,那么这条直线也和另一条垂直
-
科目: 来源: 题型:
查看答案和解析>>【题目】“宜居襄阳”是我们的共同愿景,空气质量备受人们关注.我市某空气质量监测站点检测了该区域每天的空气质量情况,统计了2013年1月份至4月份若干天的空气质量情况,并绘制了如下两幅不完整的统计图.

请根据图中信息,解答下列问题:
(1)统计图共统计了 天的空气质量情况;
(2)请将条形统计图补充完整;空气质量为“优”所在扇形的圆心角度数是 ;
(3)从小源所在环保兴趣小组4名同学(2名男同学,2名女同学)中,随机选取两名同学去该空气质量监测站点参观,则恰好选到一名男同学和一名女同学的概率是 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,将点(-2,-3)向上平移3个单位长度,则平移后的点的坐标为( )
A. (-2,0) B. (-2,1) C. (0,-2) D. (1,-1)
-
科目: 来源: 题型:
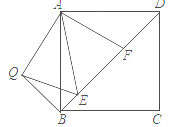
查看答案和解析>>【题目】如图,在正方形ABCD中,E、F是对角线BD上两点,且∠EAF=45°,将△ADF绕点A顺时针旋转90°后,得到△ABQ,连接EQ,求证:
(1)EA是∠QED的平分线;
(2)EF2=BE2+DF2.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如果一个实数的算术平方根与它的立方根相等,则这个数是( )
A.0B.正整数C.0和1D.1
相关试题

