【题目】如图,直线AB:y=kx+b交抛物线y=![]() 于点A、B(A在B点左侧),过点B的直线BD与抛物线只有唯一公共点,且与y轴负半轴交于点D.
于点A、B(A在B点左侧),过点B的直线BD与抛物线只有唯一公共点,且与y轴负半轴交于点D.
(1)若k=![]() ,b=2,求点A、B两点坐标;
,b=2,求点A、B两点坐标;
(2)AB交y轴于点C,若BC=CD,OC=CE,点E在y轴正半轴上,EF∥x轴,交抛物线于点F,求EF的长;
(3)在(1)的条件下,P为射线BD上一动点,PN∥y轴交抛物线于点N,交直线于点Q,PM∥AN交直线于点M,求MQ的长.

参考答案:
【答案】(1)A(﹣2,1),B(4,4);(2)2![]() ;(3)3
;(3)3![]() .
.
【解析】
(1)先表示出直线AB解析式,联立抛物线解析式,建立方程组即可求出点A,B坐标;
(2)设出直线BD解析式,联立抛物线解析式,建立方程,利用判别式为0,得出c=-a2,B(2a,a2),表示出C的坐标,利用BC=CD建立方程求出b=1,进而求出E,F的坐标,即可得出结论.
(3)先求出直线BD解析式,利用有唯一交点,求出直线BD解析式,设出点P坐标,进而表示出Q,N坐标,进而求出直线AN解析式,利用平行求出直线PM解析式,即可得出点M坐标,最后用两点间距离公式即可得出结论.
解:(1)∵k=![]() ,b=2,
,b=2,
∴直线AB:y=![]() x+2①,
x+2①,
∵抛物线![]() ②,
②,
联立①②解得,![]() 或
或![]() ,
,
∴A(﹣2,1),B(4,4);
(2)设直线BD的解析式为y=ax+c③,
∵抛物线![]() ④,
④,
联立③④得,x2﹣4ax﹣4c=0,
∵直线BD与抛物线只有唯一公共点,
∴△=16a2+16c=0,
∴c=﹣a2,
∴直线BD的解析式为y=ax﹣a2,
∴B(2a,a2),D(0,﹣a2)
∵直线AB:y=kx+b,
∴C(0,b),
∴CD2=(b+a2)2,BC2=4a2+(a2﹣b)2,
∵BC=CD,
∴(b+a2)2=4a2+(a2﹣b)2,
∴b=1,
∴OC=1,
∵OC=CE,
∴CE=1,
∴OE=2,
令y=2,则有![]() x2=2,
x2=2,
∴x=±2![]() ,
,
∴EF=2![]() ;
;
(3)由(1)知,直线AB:y=![]() x+2,A(﹣2,1),B(4,4),
x+2,A(﹣2,1),B(4,4),
∴设直线BD的解析式为y=k'(x﹣4)+4⑤,
∵抛物线![]() ⑥,
⑥,
联立⑤⑥得,x2﹣4k'x+16k'﹣16=0,
∵直线BD与抛物线只有唯一公共点,
∴△=16k'2﹣4(16k'﹣16)=0,
∴k'=2,
∴直线BD的解析式为y=2(x﹣4)+4=2x﹣4,
设P(m,2m﹣4),
∴Q(m,![]() m+2),N(m,
m+2),N(m,![]() m2),
m2),
∵A(﹣2,1),
∴直线AN的解析式为y=![]() x+
x+![]() m,
m,
∵PM∥AN,P(m,2m﹣4),
∴直线PM的解析式为y=![]() x+
x+![]() (m﹣2)(8﹣m)⑦,
(m﹣2)(8﹣m)⑦,
∵直线AB:y=![]() x+2⑧,
x+2⑧,
联立⑦⑧解得,M(m﹣6,![]() (m﹣2)),
(m﹣2)),
∵Q(m,![]() m+2),
m+2),
∴MQ2=(m﹣6﹣m)2+[![]() (m﹣2)﹣
(m﹣2)﹣![]() m+2]2=36+9=45,
m+2]2=36+9=45,
∴MQ=3![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,
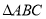 三个顶点的坐标分别为
三个顶点的坐标分别为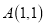 、
、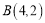 、
、 .
.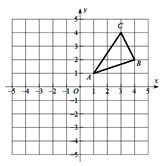
(1)若
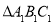 与
与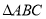 关于y轴成轴对称,则
关于y轴成轴对称,则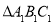 三个顶点坐标分别为
三个顶点坐标分别为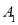 _________,
_________,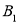 ____________,
____________,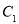 ____________;
____________;(2)若P为x轴上一点,则
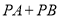 的最小值为____________;
的最小值为____________;(3)计算
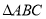 的面积.
的面积. -
科目: 来源: 题型:
查看答案和解析>>【题目】△ABC中,BC>AC,CD平分∠ACB交于AB于D,E,F分别是AC,BC边上的两点,EF交于CD于H,
(1)如图1,若∠EFC=∠A,求证:CECD=CHBC;
(2)如图2,若BH平分∠ABC,CE=CF,BF=3,AE=2,求EF的长;
(3)如图3,若CE≠CF,∠CEF=∠B,∠ACB=60°,CH=5,CE=4
 ,求
,求 的值.
的值.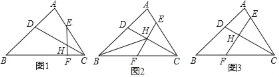
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了积极响应国家新农村建设,某市镇政府采用了移动宣讲的形式进行宣传动员.如图,笔直公路
 的一侧点
的一侧点 处有一村庄,村庄
处有一村庄,村庄 到公路
到公路 的距离为800米,假使宣讲车
的距离为800米,假使宣讲车 周围1000米以内能听到广播宣传,宣讲车
周围1000米以内能听到广播宣传,宣讲车 在公路
在公路 上沿
上沿 方向行驶时:
方向行驶时:
(1)请问村庄能否听到宣传,并说明理由;
(2)如果能听到,已知宣讲车的速度是每分钟300米,那么村庄总共能听到多长时间的宣传?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在
 中,
中,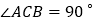 ,
, ,在
,在 上取一点
上取一点 ,在
,在 上取一点
上取一点 ,使
,使 ,过点
,过点 作
作 于点
于点 .交
.交 于点
于点 ,若
,若 ,
, ,则
,则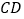 的长为________.
的长为________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形
 是菱形,
是菱形, 在
在 上,
上, 在
在 延长线上,
延长线上, 和
和 相交于点
相交于点 ,若
,若 ,
, ,
, 的长为
的长为 ,则菱形
,则菱形 的面积为________.
的面积为________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形ABCD为平行四边形,延长AD到E,使DE=AD,连接EB,EC,DB.添加一个条件,不能使四边形DBCE成为矩形的是( )

(A)AB=BE (B)BE⊥DC (C)∠ADB=90° (D)CE⊥DE
相关试题

