【题目】如图,在△ABC中,AB=AC,以AB为直径的圆交AC于点D,交BC于点E,延长AE至点F,使EF=AE,连接FB,FC.
(1)求证:四边形ABFC是菱形;
(2)若AD=7,BE=2,求半圆和菱形ABFC的面积.

参考答案:
【答案】(1)证明见解析;(2)![]()
【解析】(1)根据对角线相互平分的四边形是平行四边形,证明是平行四边形,再根据邻边相等的平行四边形是菱形即可证明;
(2)设CD=x,连接BD.利用勾股定理构建方程即可解决问题.
(1)证明:∵AB是直径,
∴∠AEB=90°,
∴AE⊥BC,
∵AB=AC,
∴BE=CE,
∵AE=EF,
∴四边形ABFC是平行四边形,
∵AC=AB,
∴四边形ABFC是菱形.
(2)设CD=x.连接BD.
∵AB是直径,
∴∠ADB=∠BDC=90°,
∴AB2﹣AD2=CB2﹣CD2,
∴(7+x)2﹣72=42﹣x2,
解得x=1或﹣8(舍弃)
∴AC=8,BD=![]() =
=![]() ,
,
∴S菱形ABFC=8![]() .
.

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知关于x的方程x2+ax+a-2=0.
(1)求证:不论a取何实数,该方程都有两个不相等的实数根;
(2)若该方程的一个根为1,求a的值及该方程的另一根.
-
科目: 来源: 题型:
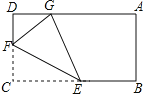
查看答案和解析>>【题目】如图,在长方形ABCD中,点E,F分别是BC,DC上的动点.沿EF 折叠△CEF,使点C的对称点G落在AD上,若AB=3,BC=5,求CF的取值范围.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在△ABC 中,AB=AC,MN垂直平分AB分别交AB、BC于M、M,如果△ACN是等腰三角形,那么∠B的大小是______________________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】随着人们环保意识的不断增强,我市家庭电动自行车的拥有量逐年增加.据统计,某小区2014年底拥有家庭电动自行车125辆,2016年底家庭电动自行车的拥有量达到180辆.
(1)若该小区2014年底到2017年底家庭电动自行车拥有量的年平均增长率相同,则该小区到2017年底电动自行车将达到多少辆?
(2)为了缓解停车矛盾,该小区决定投资3万元再建若干个停车位,据测算,建造费用分别为室内车位1000元/个,露天车位200元/个.考虑到实际因素,计划露天车位的数量不少于室内车位的2倍,但不超过室内车位的2.5倍,则该小区最多可建两种车位各多少个?试写出所有可能的方案.
-
科目: 来源: 题型:
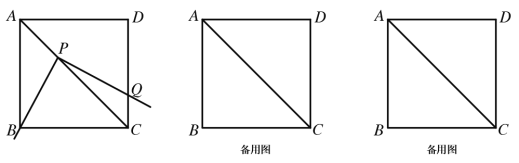
查看答案和解析>>【题目】将一把三角尺放在边长为2的正方形ABCD上(正方形四个内角为90°,四边都相等),并使它的直角顶点P在对角线AC上滑动,直角的一边始终经过点B,另一边与射线DC交于点Q。
探究:(1)当点Q在边CD 上时,线段PQ 与线段PB之间有怎样的大小关系?试证明你观察得到结论;
(2)当点Q在边CD 上时,如果四边形 PBCQ 的面积为1,求AP长度;
(3)当点P在线段AC 上滑动时,△PCQ 是否可能成为等腰三角形?如果可能,指出所有能使△PCQ 成为等腰三角形的点Q的位置,并求出相应的AP的长;如果不可能,试说明理由。
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABD≌△CDB,且AB,CD是对应边.下面四个结论中不正确的是( )

A. △ABD和△CDB的面积相等B. △ABD和△CDB的周长相等
C. ∠A+∠ABD=∠C+∠CBDD. AD∥BC,且AD=BC
相关试题

