【题目】如图,在△ABC中,∠C=90°,D,F是AB边上的两点,以DF为直径的⊙O与BC相交于点E,连接EF,∠OFE=![]() ∠A.
∠A.
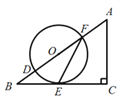
(1)求证:BC是⊙O的切线;
(2)若sinB=![]() ,求∠FEC。
,求∠FEC。
参考答案:
【答案】(1)证明见解析;(2)60°
【解析】试题分析:(1)首先连接OE,由在△ABC中,∠C=90°,FG⊥BC,可得FG∥AC,又由∠OFE=![]() ∠A,易得EF平分∠BFG,继而证得OE∥FG,证得OE⊥BC,则可得BC是⊙O的切线;
∠A,易得EF平分∠BFG,继而证得OE∥FG,证得OE⊥BC,则可得BC是⊙O的切线;
(2)由sinB=![]() 得,∠B=30°,从而∠A=60°,由∠OFE=
得,∠B=30°,从而∠A=60°,由∠OFE=![]() ∠A得∠OFE=30°
∠A得∠OFE=30°
故得∠FEC=60°
试题解析:(1)连接OE,
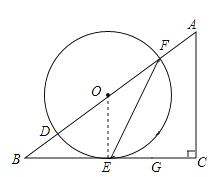
∵在△ABC中,∠C=90°,FG⊥BC,
∴∠BGF=∠C=90°,
∴FG∥AC,
∴∠OFG=∠A,
∴∠OFE=![]() ∠OFG,
∠OFG,
∴∠OFE=∠EFG,
∵OE=OF,
∴∠OFE=∠OEF,
∴∠OEF=∠EFG,
∴OE∥FG,
∴OE⊥BC,
∴BC是⊙O的切线;
(2)在RtΔABC中,sinB=![]()
∴∠B=30°
∴∠A=60°
∵∠OFE=![]() ∠A,
∠A,
∴∠OFE=30°
∴∠FEC=30°+30°=60°
-
科目: 来源: 题型:
查看答案和解析>>【题目】若
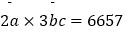 ,其中a,b,c代表非零数字,则
,其中a,b,c代表非零数字,则 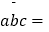 ;
; -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,∠C=45°,∠B=45°+2
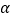 ,∠BAC=45°+3
,∠BAC=45°+3 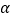 ,AE平分∠BAD,则∠CAE=;
,AE平分∠BAD,则∠CAE=;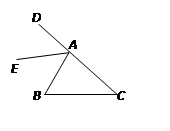
-
科目: 来源: 题型:
查看答案和解析>>【题目】己知直线AB及AB外一点P,若过点P作一直线与AB平行,那么这样的直线( )
A. 有且只有一条
B. 有两条
C. 不存在
D. 无数条
-
科目: 来源: 题型:
查看答案和解析>>【题目】大于1的正整数m的三次幂可“分裂”成若干个连续奇数的和,如23=3+5,33=7+9+11,43=13+15+17+19,…若m3分裂后,其中有一个奇数是2013,则m的值是()
A.43B.44C.45D.46
-
科目: 来源: 题型:
查看答案和解析>>【题目】等腰三角形的两边长分别为4厘米和9厘米,则这个三角形的周长为___________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列说法中
①两点之间,直线最短;
②经过直线外一点,能作一条直线与这条直线平行;
③和已知直线垂直的直线有且只有一条;
④在平面内过一点有且只有一条直线垂直于已知直线.
正确的是__________.(只需填写序号)
相关试题

