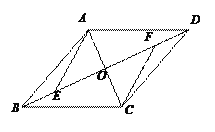
【题目】如图,在□ABCD中,AC、BD相交于点O,点E、F在BD上,且BE=DF.连
接AE、CF.
(1)求证△AOE≌△COF;
(2)若AC⊥EF,连接AF、CE,判断四边形AECF的形状,并说明理由.
参考答案:
【答案】见解析
【解析】分析:(1)由平行四边形的性质可得,OB=OD,OA=OC,再由OB-BE=OD-DF,得到OE=OF,又∠AOE=∠COF,可得△AOE≌△COF;(2)利用对角线互相垂直的平行四边形是菱形判定即可.
详解:(1)证明:∵四边形ABCD是平行四边形,
∴OB=OD,OA=OC .
又BE=DF,
∴OB-BE=OD-DF.
∴OE=OF.
又∠AOE=∠COF,
∴△AOE≌△COF.
(2)解:四边形AECF是菱形.
理由如下:
∵OA=OC,OE=OF.
∴四边形AECF是平行四边形.
又AC⊥EF,
∴四边形AECF是菱形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某校积极开展“阳光体育进校园”活动,决定开设 A:乒乓球,B:篮球,C:跑步,D:跳绳四种运动项目,规定每个学生必须参加一项活动。学校为了了解学生最喜欢哪一种运动项目,设计了以下四种调查方案.
方案一:调查该校七年级女生喜欢的运动项目
方案二:调查该校每个班级学号为 5 的倍数的学生喜欢的运动项目
方案三:调查该校书法小组的学生喜欢的运动项目
方案四:调查该校田径队的学生喜欢的运动项目
(1)上面的调查方案最合适的是 ;
学校体育组采用了(1)中的方案,将调查的结果绘制成如下两幅不完整的统计图表.
最喜欢的运动项目人数调查统计表 最喜欢的运动项目人数分布统计图


请你结合图表中的信息解答下列问题:
(2)这次抽样调查的总人数是 ,m= ;
(3)在扇形统计图中,A 项目对应的圆心角的度数为 ;
(4)已知该校有 1200 名学生,请根据调查结果估计全校学生最喜欢乒乓球的人数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】现有a枚棋子,按图1的方式摆放时刚好围成m个小正方形,按图2的方式摆放刚好围成2n个小正方形。
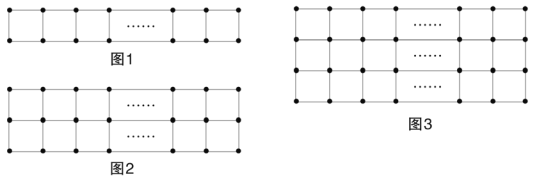
(1)用含m的代数式表示a,有a= ;用含n的代数式表示a,有a= ;
(2)若这a枚棋子按图3的方式摆放恰好围成3p个小正方形,
①P的值能取7吗?请说明理由;
②直接写出a的最小值:
-
科目: 来源: 题型:
查看答案和解析>>【题目】在数轴上点A表示-3,点B表示4.
(1)点A与点B之间的距离是 ;
(2)我们知道,在数轴上|a|表示数a所对应的点到原点的距离,你能说明
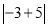 在数轴上表示的意义吗?
在数轴上表示的意义吗?(3)在数轴上点P表示的数为x,是否存在这样的点P,使2PA+PB=12?若存在,请求出相应的x;若不存在,请说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】某校组织九年级学生参加汉字听写大赛,并随机抽取部分学生成绩作为样本进行分析,绘制成如下的统计表:


请根据所给信息,解答下列问题:
(1)a=__________,b=__________;
(2)请补全频数分布直方图;
(3)已知该年级有400名学生参加这次比赛,若成绩在90分以上(含90分)的为优,估计该年级成绩为优的有多少人?
-
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙两名同学参加1 000米比赛,由于参赛选手较多,将选手随机分A、B、C三组进行比赛.
(1)甲同学恰好在A组的概率是________;
(2)求甲、乙两人至少有一人在B组的概率.
-
科目: 来源: 题型:
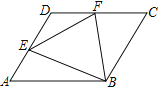
查看答案和解析>>【题目】□ABCD中,∠A=60°,点E、F分别在边AD、DC上,DE=DF,且∠EBF=60°.若AE=2,FC=3,则EF的长度为( )
A.
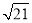 B.
B. 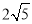 C.
C. 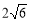 D. 5
D. 5
相关试题

