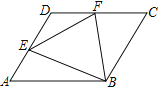
【题目】□ABCD中,∠A=60°,点E、F分别在边AD、DC上,DE=DF,且∠EBF=60°.若AE=2,FC=3,则EF的长度为( )
A. ![]() B.
B. ![]() C.
C. ![]() D. 5
D. 5
参考答案:
【答案】A
【解析】
由DE=DF,AE=2,FC=3可知AB-BC=1,过点E作EM⊥AB于M,根据30°角所对的直角等于斜边的一半可得AM=1,进而得出BM=BC,将△BEM顺时针旋转120°得△BEN,连接FN,可证△BEF≌△BFN,即可得出EF=FN,过点N作NG⊥DC交DC的延长线于点G,利用勾股定理即可求出答案.
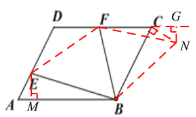
解:过点E作EM⊥AB于M,
在Rt△AEM中,∠A=60°,
∴∠AEM=30°,
∴AM=![]() AE=1,
AE=1,
∴ME=![]() ,
,
又∵DE=DF,AE=2,FC=3,
∴DC-AD=1,即AB-BC=1,
∴BM=BC,
将△BEM顺时针旋转120°得△BEN,连接FN,则CN=EM=![]() ,BE=BN,
,BE=BN,
∵∠EBF=60°,∠EBN=120°,
∴∠NBF=60°,
∴∠EBF=∠NBF
又∵BE=BN,BF=BF,
∴△BEF≌△BFN,
∴EF=FN,
过点N作NG⊥DC交DC的延长线于点G,
∵∠GCN=180°-60°-90°=30°,
∴NG=![]() NC=
NC=![]()
∴CG=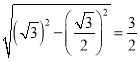
∴FG=3+![]() =
=![]()
∴FN=
∴EF=![]()
故答案为![]() .
.
-
科目: 来源: 题型:
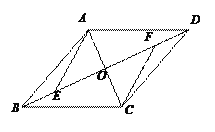
查看答案和解析>>【题目】如图,在□ABCD中,AC、BD相交于点O,点E、F在BD上,且BE=DF.连
接AE、CF.
(1)求证△AOE≌△COF;
(2)若AC⊥EF,连接AF、CE,判断四边形AECF的形状,并说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某校组织九年级学生参加汉字听写大赛,并随机抽取部分学生成绩作为样本进行分析,绘制成如下的统计表:


请根据所给信息,解答下列问题:
(1)a=__________,b=__________;
(2)请补全频数分布直方图;
(3)已知该年级有400名学生参加这次比赛,若成绩在90分以上(含90分)的为优,估计该年级成绩为优的有多少人?
-
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙两名同学参加1 000米比赛,由于参赛选手较多,将选手随机分A、B、C三组进行比赛.
(1)甲同学恰好在A组的概率是________;
(2)求甲、乙两人至少有一人在B组的概率.
-
科目: 来源: 题型:
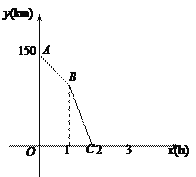
查看答案和解析>>【题目】一辆货车从甲地出发以50 km/h的速度匀速驶往乙地,行驶1 h后,一辆轿车从乙地出发沿同一条路匀速驶往甲地.轿车行驶0.8 h后两车相遇.图中折线ABC表示两车之间的距离y(km)与货车行驶时间x(h)的函数关系.
(1)甲乙两地之间的距离是__________ km,轿车的速度是_________ km/h;
(2)求线段BC所表示的函数表达式;
(3)在图中画出货车与轿车相遇后的y(km)与x(h)的函数图像.
-
科目: 来源: 题型:
查看答案和解析>>【题目】预习了“线段、射线、直线”一节的内容后,乐乐所在的小组,对如图展开了激烈的讨论,下列说法不正确的是( )

A. 直线AB与直线BA是同一条直线
B. 射线OA与射线AB是同一条射线
C. 射线OA与射线OB是同一条射线
D. 线段AB与线段BA是同一条线段
-
科目: 来源: 题型:
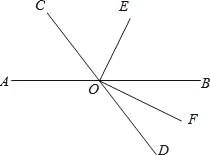
查看答案和解析>>【题目】如图,直线AB与CD相交于O.OF是∠BOD的平分线,OE⊥OF.
(1)若∠BOE比∠DOF大38°,求∠DOF和∠AOC的度数;
(2)试问∠COE与∠BOE之间有怎样的大小关系?请说明理由.
(3)∠BOE的余角是 ,∠BOE的补角是 .
相关试题

