Question

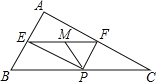
【题目】如图，在△ABC中，∠BAC=90°，AB=3，AC=4，P为边BC上一动点，PE⊥AB于E，PF⊥AC于F，M为EF的中点，则PM的最小值为（ ）

A．1.2 B．1.3 C．1.4 D．2.4

Answer 1

【答案】A

【解析】

试题分析：先求证四边形AFPE是矩形，再根据直线外一点到直线上任一点的距离，垂线段最短，利用相似三角形对应边成比例即可求得AP最短时的长，然后即可求出PM最短时的长．

解：连结AP，如图所示：

∵∠BAC=90°，AB=3，AC=4，

∴BC==5，

∵PE⊥AB，PF⊥AC，

∴四边形AFPE是矩形，

∴EF=AP．

∵M是EF的中点，

∴PM=AP，

根据直线外一点到直线上任一点的距离，垂线段最短，

即AP⊥BC时，AP最短，同样PM也最短，

∴当AP⊥BC时，AP==2.4，

∴AP最短时，AP=2.4，

∴当PM最短时，PM=AP=1.2．

故选A．