【题目】如图在直角坐标系中,已知A(0,a),B(b,0)C(3,c)三点,若a,b,c满足关系式:|a﹣2|+(b﹣3)2+![]() =0.
=0.
(1)求a,b,c的值.
(2)求四边形AOBC的面积.
(3)是否存在点P(x,﹣![]() x),使△AOP的面积为四边形AOBC的面积的两倍?若存在,求出点P的坐标,若不存在,请说明理由.
x),使△AOP的面积为四边形AOBC的面积的两倍?若存在,求出点P的坐标,若不存在,请说明理由.

参考答案:
【答案】(1)a=2,b=3,c=4;(2)9;(3)存在点P(18,﹣9)或(﹣18,9),使△AOP的面积为四边形AOBC的面积的两倍.
【解析】
(1)根据“几个非负数相加和为0,则每一个非负数的值均为0”解出a,b,c的值;
(2)由点A、O、B、C的坐标可得四边形AOBC为直角梯形,根据直角梯形的面积公式计算即可;
(3)设存在点P(x,﹣![]() x),使△AOP的面积为四边形AOBC的面积的两倍.根据面积列出方程
x),使△AOP的面积为四边形AOBC的面积的两倍.根据面积列出方程![]() ×2×|x|=|x|=2×9,解方程即可.
×2×|x|=|x|=2×9,解方程即可.
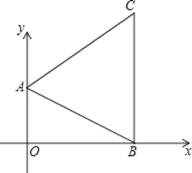
解:(1)∵|a﹣2|+(b﹣3)2+![]() =0,
=0,
∴a﹣2=0,b﹣3=0,c﹣4=0,
∴a=2,b=3,c=4;
(2)∵A(0,2),O(0,0),B(3,0),C(3,4);
∴四边形AOBC为直角梯形,且OA=2,BC=4,OB=3,
∴四边形AOBC的面积=![]() ×(OA+BC)×OB=
×(OA+BC)×OB=![]() ×(2+4)×3=9;
×(2+4)×3=9;
(3)设存在点P(x,﹣![]() x),使△AOP的面积为四边形AOBC的面积的两倍.
x),使△AOP的面积为四边形AOBC的面积的两倍.
∵△AOP的面积=![]() ×2×|x|=|x|,
×2×|x|=|x|,
∴|x|=2×9,
∴x=±18
∴存在点P(18,﹣9)或(﹣18,9),
使△AOP的面积为四边形AOBC的面积的两倍.
故答案为:(1)a=2,b=3,c=4;(2)9;(3)存在点P(18,﹣9)或(﹣18,9),使△AOP的面积为四边形AOBC的面积的两倍.
-
科目: 来源: 题型:
查看答案和解析>>【题目】完成推理填空:如图在△ABC中,已知∠1+∠2=180°,∠3=∠B,试说明∠AED=∠C.
解:∵∠1+∠EFD=180°(邻补角定义),∠1+∠2=180°(已知 )
∴ (同角的补角相等)①
∴ (内错角相等,两直线平行)②
∴∠ADE=∠3( )③
∵∠3=∠B( )④
∴ (等量代换)⑤
∴DE∥BC( )⑥
∴∠AED=∠C( )⑦

-
科目: 来源: 题型:
查看答案和解析>>【题目】在读书月活动中,学校准备购买一批课外读物.为使课外读物满足同学们的需求,学校就“我最喜爱的课外读物”从文学、艺术、科普和其他四个类别进行了抽样调查(每位同学只选一类),如图是根
据调查结果绘制的两幅不完整的统计图.

请你根据统计图提供的信息,解答下列问题:
(1)本次调查中,一共调查了 名同学;
(2)条形统计图中,m= ,n= ;
(3)扇形统计图中,艺术类读物所在扇形的圆心角是 度;
(4)学校计划购买课外读物6000册,请根据样本数据,估计学校购买其他类读物多少册比较合理?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,抛物线y=﹣x2+bx+c与x轴交于A、B两点(点A在点B的左侧),点A的坐标为(﹣1,0),与y轴交于点C(0,3),作直线BC.动点P在x轴上运动,过点P作PM⊥x轴,交抛物线于点M,交直线BC于点N,设点P的横坐标为m.
(Ⅰ)求抛物线的解析式和直线BC的解析式;
(Ⅱ)当点P在线段OB上运动时,求线段MN的最大值;
(Ⅲ)当以C、O、M、N为顶点的四边形是平行四边形时,直接写出m的值.

-
科目: 来源: 题型:
查看答案和解析>>【题目】为提高饮水质量,越来越多的居民选购家用净水器.我市飞龙商场抓住商机,从厂家购进了A、B两种型号家用净水器共100台,A型号家用净水器进价是150元/台,B型号家用净水器进价是250元/台,购进两种型号的家用净水器共用去19000 元.
(1)求A、B两种型号家用净水器各购进了多少台;
(2)为使每台B型号家用净水器的毛利润是A型号的2倍,且保证售完这100台家用净水器的毛利润不低于5600元,求每台A型号家用净水器的售价至少是多少元? (注: 毛利润=售价一进价) .
-
科目: 来源: 题型:
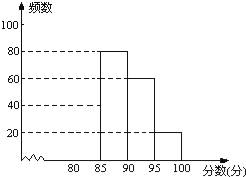
查看答案和解析>>【题目】某校组织了“安全在我心中”知识竞赛活动.根据获奖同学在竞赛中的成绩制成的统计图表如下:
分数段
频数
频率
80≤x<85
x
0.2
85≤x<90
80
y
90≤x<95
60
0.3
95≤x<100
20
0.1
根据以上图表提供的信息,解答下列问题:
(1)写出表中x,y的数值;
(2)请补全频数分布直方图;
(3)如果成绩在95分以上(含95分)的可以获得特等奖,那么获奖的同学获得特等奖的概率是多少?
(4)获奖成绩的中位数落在哪个分数段?
-
科目: 来源: 题型:
查看答案和解析>>【题目】将背面完全相同,正面上分别写有数字1,2,3,4的四张卡片混合后,小明从中随机地抽取一张,把卡片上的数字做为被减数,将形状、大小完全相同,分别标有数字1,2,3的三个小球混合后,小华从中随机地抽取一个,把小球上的数字做为减数,然后计算出这两个数的差.
(1)请你用画树状图或列表的方法,求这两数差为0的概率;
(2)小明与小华做游戏,规则是:若这两数的差为非负数,则小明赢;否则,小华赢.你认为该游戏公平吗?请说明理由.如果不公平,请你修改游戏规则,使游戏公平.
相关试题

