搜索
【题目】如图，四边形ABCD是矩形，把矩形沿AC折叠，点B落在点E处，AE与DC的交点为O，连接DE．
（1）求证：△ADE≌△CED；
（2）求证：DE∥AC．
参考答案：
【答案】（1）证明见解析；（2）证明见解析.
【解析】试题分析：（1）根据矩形的性质和折叠对称的性质，由SSS可证明ADE≌CED.
（2）根据全等的性质和折叠对称的性质，可求得∠OAC =∠DEA，从而根据平行的判定得出结论.
试题解析：（1）∵ 四边形ABCD是矩形，∴AD=BC，AB=CD.
又∵AC是折痕，∴BC =" CE" =" AD" ，AB =" AE" =" CD" .
又∵DE = ED，∴ΔADE ≌ΔCED（SSS）.
（2）∵ΔADE ≌ΔCED，∴∠EDC =∠DEA.
又∵ΔACE与ΔACB关于AC所在直线对称，∴∠OAC =∠CAB.
又∵∠OCA =∠CAB，∴∠OAC =∠OCA.
∴2∠OAC = 2∠DEA. ∴∠OAC =∠DEA.
∴DE∥AC.
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，直线l：y=﹣x+1与x轴，y轴分别交于A，B两点，点P，Q是直线l上的两个动点，且点P在第二象限，点Q在第四象限，∠POQ=135°．
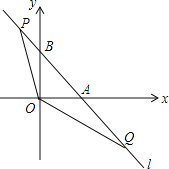
（1）求△AOB的周长；
（2）设AQ=t＞0，试用含t的代数式表示点P的坐标；
（3）当动点P，Q在直线l上运动到使得△AOQ与△BPO的周长相等时，记tan∠AOQ=m，若过点A的二次函数y=ax2+bx+c同时满足以下两个条件：
①6a+3b+2c=0；
②当m≤x≤m+2时，函数y的最大值等于
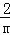，求二次项系数a的值． -
科目： 来源： 题型：
查看答案和解析>>【题目】下列语句中，属于命题的是（ ）
A.等角的余角相等
B.两点之间，线段最短吗
C.连接P、Q两点
D.花儿会不会在春天开放 -
科目： 来源： 题型：
查看答案和解析>>【题目】点到直线的距离是指这点到这条直线的
A、垂线段B、垂线的长
C、长度D、垂线段的长度
-
科目： 来源： 题型：
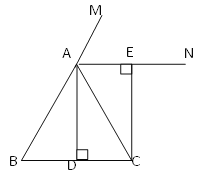
查看答案和解析>>【题目】如图所示，在△ABC中，AD平分∠BAC，AD⊥BC，垂足为D，AN是△ABC外角∠CAM的平分线，CE⊥AN，垂足为E.
（1）求证：四边形ADCE是矩形；
（2）当△ABC满足什么条件时，四边形ADCE是正方形？给出证明.
-
科目： 来源： 题型：
查看答案和解析>>【题目】若m﹣n=﹣1，则（m﹣n）2﹣2m+2n的值是（ ）
A.3
B.2
C.1
D.﹣1 -
科目： 来源： 题型：
查看答案和解析>>【题目】已知点A、B、C在同一直线上，AB=4cm，AC=3cm,则B、C两点之间的距离是_______cm。
相关试题
