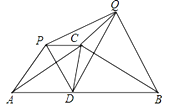
【题目】如图,等腰△ABC中,CA=CB=6,∠ACB=120°,点D在线段AB上运动(不与A、B重合),将△CAD与△CBD分别沿直线CA、CB翻折得到△CAP与△CBQ,给出下列结论:
①CD=CP=CQ;②∠PCQ为定值;③△PCQ面积的最小值为![]() ;④当点D在AB的中点时,△PDQ是等边三角形,其中正确结论的个数为( )
;④当点D在AB的中点时,△PDQ是等边三角形,其中正确结论的个数为( )
A. 1 B. 2 C. 3 D. 4
参考答案:
【答案】C
【解析】①由折叠直接得到结论;②由折叠的性质求出∠ACP +∠BCQ=120°,再用周角的定义求出∠PCQ=120°;③先作出△PCQ的边PC上的高,用三角函数求出QE=![]() CQ,得到S△PCQ =
CQ,得到S△PCQ =![]() CD2,判断出△PCQ面积最小时,点D的位置,再求△PCQ面积的最小值即可;④先判断出△APD 是等边三角形,△BDQ是等边三角形,再求出∠PDQ=60°,即可得结论.
CD2,判断出△PCQ面积最小时,点D的位置,再求△PCQ面积的最小值即可;④先判断出△APD 是等边三角形,△BDQ是等边三角形,再求出∠PDQ=60°,即可得结论.
① ∵将△ CAD 与△ CBD 分别沿直线 CA、CB 翻折得到△CAP与△CBQ ,
∴CP=CD=CQ,
∴ ①正确;
② ∵将△ CAD与△CBD 分别沿直线CA、CB翻折得到△CAP 与△CBQ ,
∴∠ACP=∠ACD,∠BCQ=∠BCD ,
∴∠ACP +∠BCQ=∠ACD +∠BCD=∠ACB=120°,
∴∠ PCQ=360°﹣(∠ACP +BCQ +∠ACB ) =360°﹣(120°+120°) =120°,
∴∠ PCQ 的大小不变;
∴ ② 正确;
③ 如图,过点Q作QE ⊥ PC 交PC延长线于 E ,

∵∠PCQ=120°,
∴∠QCE=60°,
在 Rt△QCE 中, sin∠QCE=![]() ,
,
∴QE=CQ×sin∠QCE=CQ×sin60°=![]() CQ ,
CQ ,
∵CP=CD=CQ,
∴ S△PCQ =![]() ×CP×QE=
×CP×QE=![]() CP×CQ=
CP×CQ=![]() CD 2,
CD 2,
∴ CD 最短时,S △ PCQ最小,
即:CD ⊥ AB 时,CD最短,
过点 C 作 CF ⊥ AB,此时 CF 就是最短的 CD ,
∵ AC=BC=6,∠ ACB=120°,
∴∠ ABC=30°,
∴CF=![]() BC=3,
BC=3,
即:CD最短为3,
∴ S △ PCQ最小 =![]() ,
,
∴ ③错误;
④ ∵将△CAD与△CBD 分别沿直线CA、CB翻折得到△CAP与△CBQ ,
∴ AD=AP,∠ DAC=∠ PAC,
∵∠ DAC=30°,
∴∠ APD=60°,
∴△ APD是等边三角形,
∴ PD=AD,∠ ADP=60°,
同理:△ BDQ是等边三角形,
∴ DQ=BD,∠ BDQ=60°,
∴∠ PDQ=60°,
∵当点D在AB的中点,
∴AD=BD,
∴PD=DQ,
∴△DPQ 是等边三角形.
∴ ④正确.
正确的答案为:①②④ .
故选C.
-
科目: 来源: 题型:
查看答案和解析>>【题目】
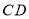 是
是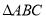 的高.
的高.(1)如图1,若
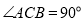 ,
,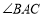 的平分线
的平分线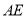 交
交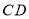 于点
于点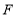 ,交
,交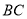 于点
于点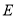 ,求证:
,求证: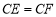 ;
;(2)如图2,若
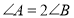 ,
,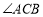 的平分线
的平分线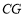 交
交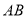 于点
于点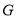 ,求
,求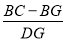 的值;
的值;(3)如图3,若
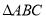 是以
是以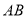 为斜边的等腰直角三角形,再以
为斜边的等腰直角三角形,再以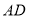 为斜边作等腰
为斜边作等腰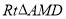 ,
,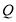 是
是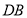 的中点,连接
的中点,连接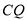 、
、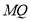 ,试判断线段
,试判断线段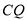 与
与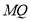 的关系,并给出证明.
的关系,并给出证明.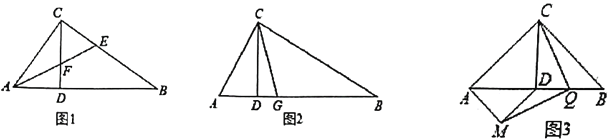
-
科目: 来源: 题型:
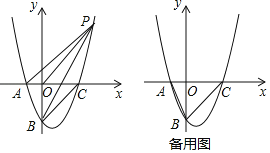
查看答案和解析>>【题目】已知抛物线y=
 x2+bx+c经过点A(﹣2,0),B(0、﹣4)与x轴交于另一点C,连接BC.
x2+bx+c经过点A(﹣2,0),B(0、﹣4)与x轴交于另一点C,连接BC.(1)求抛物线的解析式;
(2)如图,P是第一象限内抛物线上一点,且S△PBO=S△PBC,求证:AP∥BC;
(3)在抛物线上是否存在点D,直线BD交x轴于点E,使△ABE与以A,B,C,E中的三点为顶点的三角形相似(不重合)?若存在,请求出点D的坐标;若不存在,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知正方形ABCD与正方形CEFG,M是AF的中点,连接DM,EM.
(1)如图1,点E在CD上,点G在BC的延长线上,请判断DM,EM的数量关系与位置关系,并直接写出结论;
(2)如图2,点E在DC的延长线上,点G在BC上,(1)中结论是否仍然成立?请证明你的结论;
(3)将图1中的正方形CEFG绕点C旋转,使D,E,F三点在一条直线上,若AB=13,CE=5,请画出图形,并直接写出MF的长.

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知多项式(x2+mx﹣
 y+3)﹣(3x﹣2y+1﹣nx2).
y+3)﹣(3x﹣2y+1﹣nx2).(1)若多项式的值与字母x的取值无关,求m,n的值;
(2)先化简多项式3(m2﹣mn﹣n2)﹣(3m2+mn+n2),再求它的值;
(3)在(1)的条件下,求(n+m2)+(2n+
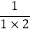 m2)+(3n+
m2)+(3n+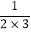 m2)+…+(9n+
m2)+…+(9n+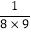 m2).
m2). -
科目: 来源: 题型:
查看答案和解析>>【题目】把正整数1,2,3,4……,排列成如图1所示的一个表,从上到下分别称为第1行、第2行、…,从左到右分别称为第1列、第2列、…….用图2所示的方框在图1中框住16个数,把其中没有被阴影覆盖的四个数分别记为A、B、C、D.设A=x.

(1)在图1中,2018排在第 行第 列;排在第m行第n列的数为 ,其中m≥1,1≤n≤8,且都是正整数;(直接写出答案)
(2)若A+2B+3D=357,求出C所表示的数;
(3)在图(2)中,被阴影覆盖的这些数的和能否为4212?如果能,请求出这些数中最大的数,如果不能,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】比较下列各对数的大小:
(1)
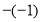 ________
________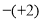 ;(2)
;(2)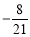 ________
________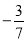 ;(3)
;(3) ________
________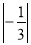 ;(4)
;(4)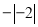 ________
________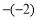
相关试题

