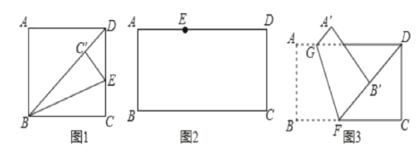
【题目】(1)如图1,将矩形ABCD折叠,使BC落在对角线BD上,折痕为BE,点C落在点C'处,若∠ADB=46°,则∠DBE的度数为______.
(2)小明手中有一张矩形纸片ABCD,AB=4,AD=9.
(画一画)
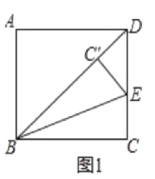
如图2,点E在这张矩形纸片的边AD上,将纸片折叠,使AB落在CE所在直线上,折痕设为MN(点M,N分别在边AD,BC上),利用直尺和圆规画出折痕MN(不写作法,保留作图痕迹,并用黑色水笔把线段描清楚);
(算一算)
如图3,点F在这张矩形纸片的边BC上,将纸片折叠,使FB落在射线FD上,折痕为GF,点A,B分别落在点A',B'处,若AG=![]() ,求B'D的长;
,求B'D的长;
参考答案:
【答案】(1)23(2)【画一画】画图见解析;【算一算】DB`=3
【解析】
(1)根据矩形性质可得AD∥BC,从而可得∠ADB=∠DBC=46°,再根据翻折的性质即可求得∠DBE的度
(2)画一画:连接CE并延长交BA的延长线与点G,利用尺规作图画出∠BGC的角平分线即可得抓痕MN,
算一算:由已知可得GD=![]() ,根据矩形的性质及翻折的性质可得∠DFG=∠DGF,从而可得DF=DG=
,根据矩形的性质及翻折的性质可得∠DFG=∠DGF,从而可得DF=DG=![]() ,在Rt△CDE中,根据勾股定理可求得CF=
,在Rt△CDE中,根据勾股定理可求得CF=![]() ,根据BF=BC-CF求得BF的长,再根据翻折的性质继而可求得DB`的长即可
,根据BF=BC-CF求得BF的长,再根据翻折的性质继而可求得DB`的长即可
(1)如图1中,
∵四边形ABCD是矩形,
∴AD//BC,
∴∠ADB=∠DBC=46°,
由翻折不变性可知,∠DBE=∠EBC=![]() ∠DBC=23°,
∠DBC=23°,
故答案为23.
(2)【画一画】,如图2中,

【算一算】
如图3中,
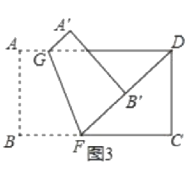
∵AG=![]() ,AD=9,
,AD=9,
∴GD=9![]() =
=![]() ,
,
∵四边形ABCD是矩形,
∴AD//BC,
∴∠DGF=∠BFG,
由翻折不变性可知,∠BFG=∠DFG,
∴∠DFG=∠DGF,
∴DF=DG=![]() ,
,
∵CD=AB=4,∠C=90°,
∴在Rt△CDF中,CF=![]() ,
,
∴BF=BCCF=![]() ,
,
由翻折不变性可知,FB=FB'=![]() ,
,
∴DB'=DFFB'=![]()
![]() =3.
=3.
-
科目: 来源: 题型:
查看答案和解析>>【题目】矩形ABCD中,CE平分∠BCD,交直线AD于点E,若CD=6,AE=2,则tan∠ACE=______.
-
科目: 来源: 题型:
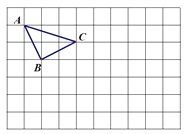
查看答案和解析>>【题目】在网格中,如图所示,请根据下列提示作图:
(1)先将△ABC向下平移3个单位长度,再向右平移4个单位长度得到△DEF(A与D,B与E,C与F分别对应);
(2)连接BD、CD,直接写出以B、C、D为顶点的三角形的面积 ;
(3)过点F作FG∥CD,交AC的延长线于点G.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(8分)如图,在平面直角坐标系中,△ABC的三个顶点的坐标分别是A(-3,2),B(-1,4),C(0,2).
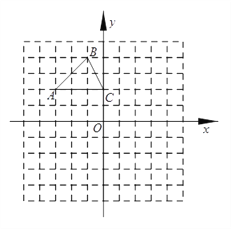
(1)将△ABC以点C为旋转中心旋转180°,画出旋转后对应的△A1B1C;
(2)平移△ABC,若A的对应点A2的坐标为(-5,-2),画出平移后的△A2B2C2;
(3)若将△A2B2C2绕某一点旋转可以得到△A1B1C,请直接写出旋转中心的坐标.
-
科目: 来源: 题型:
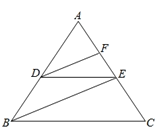
查看答案和解析>>【题目】完成下面推理过程:
如图,已知:DE∥BC,DF、BE分别平分∠ADE、∠ABC.
求证:∠FDE=∠DEB
证明:∵DE∥BC(已知)
∴∠ADE=∠ ① ( ② )
∵DF、BE分别平分∠ADE、∠ABC,(已知)
∴∠ADF=
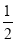 ∠ ③ ( ④ )
∠ ③ ( ④ )∠ABE=
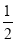 ∠ ⑥ ( ⑤ )
∠ ⑥ ( ⑤ )∴∠ADF=∠ABE(等量代换)
∴DF∥ ( ⑦ )
∴∠FDE=∠DEB( ⑧ )
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知BC∥GE,AF∥DE,∠1=50°.
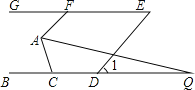
(1)求∠AFG的度数;
(2)若AQ平分∠FAC,交BC于点Q,且∠Q=15°,求∠ACB的度数.
-
科目: 来源: 题型:
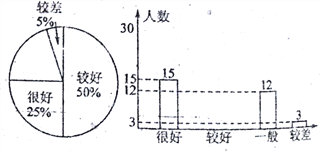
查看答案和解析>>【题目】我国北方又进入了交通事故频发的季节,为此,某校在全校2000名学生中随机抽取一部分人进行“交通安全”知识问卷调查活动,对问卷调查成绩按“很好”、“较好”、“一般”、“较差”四类汇总分析,并绘制了如下扇形统计图和条形统计图.
(1)本次活动共抽取了多少名同学?
(2)补全条形统计图;
(3)根据以上调查结果分析,估计该校2000名学生中,对“交通安全”知识了解一般的学生约有多少名?
相关试题

