【题目】矩形ABCD中,CE平分∠BCD,交直线AD于点E,若CD=6,AE=2,则tan∠ACE=______.
参考答案:
【答案】![]() 或
或![]()
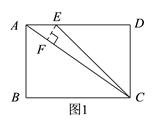
【解析】(1)如图1,当点E在线段AD上时,
∵在矩形ABCD中,AD∥BC,CE平分∠BCD,
∴∠DEC=∠BCE=∠DCE,
∴DE=CD=6,
∵AE=2,
∴AD=6+2=8,
∴在Rt△ACD中,AC=10,
过点E作EF⊥AC于点F,
则由sin∠EAF=![]() ,可得EF=
,可得EF=![]() ,AF=
,AF=![]() ,
,
∴CF=![]() ,
,
∴tan∠ACE=![]() ;
;
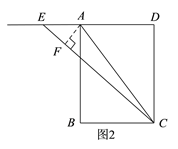
(2)如图2,当点E在DA的延长线上时,过点A作AF⊥EC于点F,
∵在矩形ABCD中,AD∥BC,CE平分∠BCD,
∴∠DEC=∠BCE=∠DCE,
∴DE=CD=6,
∵∠D=90°,
∴CE=![]() ,∠AEF=∠EAF=45°,
,∠AEF=∠EAF=45°,
∵AE=2,
∴EF=AF=![]() ,
,
∴FC=CE-EF=![]() ,
,
∴tan∠ACE=![]() .
.
综上所述,tan∠ACE=![]() 或
或![]() .
.
故答案为: ![]() 或
或![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读下面材料:如图1,圆的概念:在平面内,线段PA绕它固定的一个端点P旋转一周,另一个端点A所形成的图形叫做圆.就是说,到某个定点等于定长的所有点在同一个圆上.圆心在P(a,b),半径为r的圆的方程可以写为:(x-a)2+(y-b)2=r2.如:圆心在P(2,-1),半径为5的圆的方程为:(x-2)2+(y+1)2=25.
(1)填空: ①以A(3,0)为圆心,1为半径的圆的方程为:________; ②以B(-1,-2)为圆心,
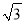 为半径的圆的方程为:________;
为半径的圆的方程为:________;(2)根据以上材料解决以下问题:
如图2,以B(-6,0)为圆心的圆与y轴相切于原点,C是☉B上一点,连接OC,作BD⊥OC垂足为D,延长BD交y轴于点E,已知sin∠AOC=
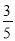 .
.①连接EC,证明EC是☉B的切线;
②在BE上是否存在一点P,使PB=PC=PE=PO,若存在,求P点坐标,并写出以P为圆心,以PB为半径的☉P的方程;若不存在,说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】早晨,小刚沿着通往学校唯一的一条路(直路)上学,途中发现忘带饭盒,停下来往家里打电话,妈妈接到电话后带上饭盒马上赶往学校,同时小刚返回,两人相遇后,小刚立即赶往学校,妈妈回家,15分钟后妈妈到家,再经过3分钟小刚到达学校,小刚始终以100米/分的速度步行,小刚和妈妈的距离y(单位:米)与小刚打完电话后的步行时间t(单位:分)之间的函数关系如图,下列四种说法中错误的是( )

A. 打电话时,小刚和妈妈的距离为1250米
B. 打完电话后,经过23分钟小刚到达学校
C. 小刚和妈妈相遇后,妈妈回家的速度为150米/分
D. 小刚家与学校的距离为2550米
-
科目: 来源: 题型:
查看答案和解析>>【题目】有甲、乙两个不透明的布袋,甲袋中有两个完全相同的小球,分别标有数字1和-2;乙袋中有三个完全相同的小球,分别标有数字-1、0和2.小丽先从甲袋中随机取出一个小球,记录下小球上的数字为x;再从乙袋中随机取出一个小球,记录下小球上的数字为y,设点A的坐标为(x,y).
(1)请用表格或树状图列出点A所有可能的坐标;
(2)求点A在反比例函数y=
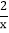 图象上的概率.
图象上的概率. -
科目: 来源: 题型:
查看答案和解析>>【题目】在网格中,如图所示,请根据下列提示作图:
(1)先将△ABC向下平移3个单位长度,再向右平移4个单位长度得到△DEF(A与D,B与E,C与F分别对应);
(2)连接BD、CD,直接写出以B、C、D为顶点的三角形的面积 ;
(3)过点F作FG∥CD,交AC的延长线于点G.
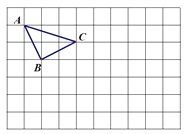
-
科目: 来源: 题型:
查看答案和解析>>【题目】(8分)如图,在平面直角坐标系中,△ABC的三个顶点的坐标分别是A(-3,2),B(-1,4),C(0,2).
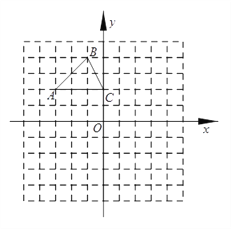
(1)将△ABC以点C为旋转中心旋转180°,画出旋转后对应的△A1B1C;
(2)平移△ABC,若A的对应点A2的坐标为(-5,-2),画出平移后的△A2B2C2;
(3)若将△A2B2C2绕某一点旋转可以得到△A1B1C,请直接写出旋转中心的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)如图1,将矩形ABCD折叠,使BC落在对角线BD上,折痕为BE,点C落在点C'处,若∠ADB=46°,则∠DBE的度数为______.
(2)小明手中有一张矩形纸片ABCD,AB=4,AD=9.
(画一画)
如图2,点E在这张矩形纸片的边AD上,将纸片折叠,使AB落在CE所在直线上,折痕设为MN(点M,N分别在边AD,BC上),利用直尺和圆规画出折痕MN(不写作法,保留作图痕迹,并用黑色水笔把线段描清楚);
(算一算)
如图3,点F在这张矩形纸片的边BC上,将纸片折叠,使FB落在射线FD上,折痕为GF,点A,B分别落在点A',B'处,若AG=
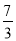 ,求B'D的长;
,求B'D的长;
相关试题

