【题目】如图,△ABC为等边三角形,∠ABC、∠ACB的平分线相交于点O,OE∥AB交BC于点E,OF∥AC交BC于点F,图中等腰三角形共有( )
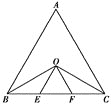
A. 6个 B. 5个 C. 4个 D. 3个
参考答案:
【答案】B
【解析】
由已知条件,首先得到∠OBC=∠OCB,利用两个角相等即为等腰三角形,得到△BOC为等腰三角形;然后在题中找出对应角相等即可.
解:∵△ABC为正三角形,∴△ABC为等腰三角形;
∵OB,OC为角平分线,∴∠OBC=∠OCB,∴△BOC为等腰三角形;
∵OE∥AB,∴∠ABO=∠BOE=∠OBE,∴△BOE为等腰三角形;
同理,△COF为等腰三角形;
∠OEF=∠OFE,∴△EOF为等腰三角形.
所以题中共有5个等腰三角形
故选:B.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在菱形ABCD中,∠ABC=60°,AB=2,点P是这个菱形内部或边上的一点,若以点P、B、C为顶点的三角形是等腰三角形,则P、D(P、D两点不重合)两点间的最短距离为 .

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知AB=AD,那么添加下列一个条件后,仍无法判定△ABC≌△ADC的是( )

A. CB=CD B. ∠BAC=∠DAC C. ∠BCA=∠DCA D. ∠B=∠D=90°
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算题
(1)计算:|﹣ |+(
|+(  )﹣1﹣2cos45°.
)﹣1﹣2cos45°.
(2)解方程: +
+  =1.
=1. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系xOy中,菱形ABCD的顶点A的坐标为(2,0),点B的坐标为(0,1),点C在第一象限,对角线BD与x轴平行.直线y=x+3与x轴、y轴分别交于点E、F.将菱形ABCD沿x轴向左平移m个单位,当点D落在△EOF的内部时(不包括三角形的边),m的取值范围是( )
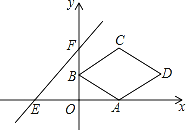
A. 4<m<6 B. 4≤m≤6 C. 4<m<5 D. 4≤m<5
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点O是△ABC内一点,连结OB、OC,并将AB、OB、OC、AC的中点D、E、F、G依次连结,得到四边形DEFG.

(1)求证:四边形DEFG是平行四边形;
(2)若M为EF的中点,OM=3,∠OBC和∠OCB互余,求DG的长度. -
科目: 来源: 题型:
查看答案和解析>>【题目】在△ABC中,AB=AC,点D是BC的中点,点E是AD上任意一点.
(1)如图1,连接BE、CE,问:BE=CE成立吗?并说明理由;
(2)如图2,若∠BAC=45°,BE的延长线与AC垂直相交于点F时,问:EF=CF成立吗?并说明理由.

相关试题

