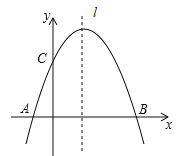
【题目】已知抛物线![]() 经过A(-1,0)、B(3,0)点,直线l是抛物线的对称轴.
经过A(-1,0)、B(3,0)点,直线l是抛物线的对称轴.
(1)求抛物线的函数关系式;
(2)在直线l上确定一点P,使△PAC的周长最小,求出点P的坐标.
参考答案:
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】
(1)将点A(-1,0)、B(3,0)代入抛物线的解析式求出a、b即可;
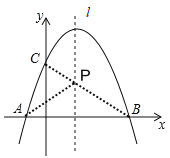
(2)由A、B关于抛物线对称轴对称可知,连接BC交对称轴于点![]() ,点
,点![]() 即为所求,求出直线BC的解析式,代入x=1即可得到点
即为所求,求出直线BC的解析式,代入x=1即可得到点![]() 的坐标;
的坐标;
解:(1)∵抛物线过点A(-1,0)、B(3,0),
∴![]() ,
,
解得:![]() ,
,
∴抛物线的解析式为:![]() ;
;
(2)由![]() 得:
得:![]() ,
,
∴![]() ,
,
又∵抛物线对称轴为:![]() ,点A关于
,点A关于![]() 对称的点为
对称的点为![]() ,
,
∴连接BC交对称轴![]() 于点
于点![]() ,点
,点![]() 即为所求,
即为所求,
设直线BC解析式为:![]() ,
,
代入![]() ,
,![]() 得:
得:![]() ,解得:
,解得:![]() ,
,
∴直线BC解析式为:![]() ,
,
当![]() 时,
时,![]() ,
,
∴![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,A、P、B、C是⊙O上的四个点,∠APC=∠CPB=60°.
(1)求证:PA+PB=PC;
(2)若BC=
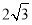 ,点P是劣弧AB上一动点(异于A、B),PA、PB是关于x的一元二次方程x2﹣mx+n=0的两根,求m的最大值.
,点P是劣弧AB上一动点(异于A、B),PA、PB是关于x的一元二次方程x2﹣mx+n=0的两根,求m的最大值.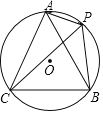
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知二次函数
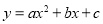 图象上部分点的横坐标
图象上部分点的横坐标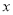 与纵坐标
与纵坐标 的对应值如表所示:
的对应值如表所示: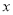
···
-3
-2
-1
0
···

···
0
-3
-4
-3
···
直接写出不等式
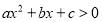 的解集是____________________.
的解集是____________________. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知二次函数
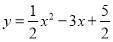 ,
,(1)该二次函数图象与x轴的交点坐标是______________;
(2)将
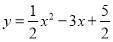 化成
化成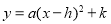 的形式_____________________,并写出顶点坐标______________.
的形式_____________________,并写出顶点坐标______________.(3)在坐标轴中画出此抛物线的大致图象;
(4)写出不等式
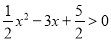 的解集___________________;
的解集___________________;
(5)当
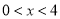 时,直接写出y的取值范围_________________.
时,直接写出y的取值范围_________________. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知二次函数
 .
.(1)证明:无论m取何值,函数图象与x轴都有两个不相同的交点;
(2)当图象的对称轴为直线x=3时,求它与x轴两交点及顶点所构成的三角形的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,以AB为直径的⊙O分别交AC、BC于点D、E,点F在AC的延长线上,且AC=CF,∠CBF=∠CFB.
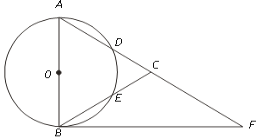
(1)求证:直线BF是⊙O的切线;
(2)若点D,点E分别是弧AB的三等分点,当AD=5时,求BF的长和扇形DOE的面积;
(3)在(2)的条件下,如果以点C为圆心,r为半径的圆上总存在不同的两点到点O的距离为5,则r的取值范围为 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】小东根据学习函数的经验,对函数
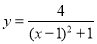 的图像与性质进行了探究,下面是小东的探究过程,请补充完整,并解决相关问题:
的图像与性质进行了探究,下面是小东的探究过程,请补充完整,并解决相关问题:(1)函数
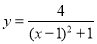 的自变量x的取值范围是__________________
的自变量x的取值范围是__________________(2)如表示y与x的几组对应值:
x
…
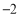
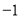
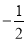
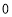
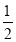
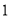
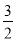
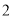
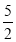
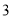
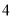
…
y
…
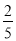
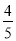
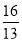
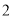
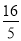
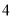
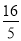
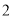
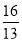
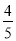
m
…
表中m的值为____________
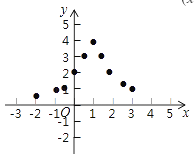
(3)如图,在平面直角坐标系中,描出了以上表中各对对应值为坐标的点,根据描出的点,画出函数
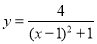 的大致图像;
的大致图像;(4)结合函数图像,请写出函数
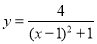 的2条性质:
的2条性质:①__________________________________________________________________________
②__________________________________________________________________________
(5)解决问题:如果函数
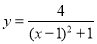 与直线
与直线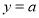 的交点有2个,那么a的取值范围是_______________________
的交点有2个,那么a的取值范围是_______________________(6)
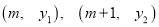 在函数图像上,若
在函数图像上,若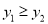 ,则m的取值范围______________
,则m的取值范围______________
相关试题

