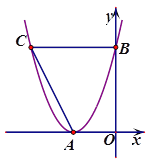
【题目】如图,已知抛物线与x轴只有一个交点A(-2,0),与y轴交于点B(0,4).
(1)求抛物线对应的函数解析式;
(2)过点B做平行于x轴的直线交抛物线与点C.
①若点M在抛物线的AB段(不含A、B两点)上,求四边形BMAC面积最大时,点M的坐标;
②在平面直角坐标系内是否存在点P,使以P、A、B、C为顶点的四边形是平行四边形,若存在直接写出所有满足条件的点P的坐标;若不存在,请说明理由.
参考答案:
【答案】(1)y=(x+2)2 (2)①点M的坐标为(-1,1) ②存在 所有满足条件的点P的坐标是(2,0)、(-6,0)、(-2,8)
【解析】(1)由已知可设抛物线对应函数的解析式为:y=a(x+2)2(a≠0),∵抛物线与y轴交于点B(0,4)
∴4=a(0+2)2
解得:a=1
∴抛物线对应的解析式为:y=(x+2)2.
(2)①如图1中,设点M的坐标为(m,(m+2)2),其中﹣2<m<0,则N点坐标(m,0).
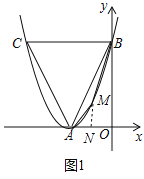
∵A、B、C是定点,∴若要四边形BMAC的面积最大,只要BMA的面积最大即可.
过M做MN⊥x轴于点N,则
S△AOB=![]() OAOB=
OAOB=![]() ×2×4=4
×2×4=4
S△AMN=![]() ANMN=
ANMN=![]() ×[m﹣(﹣2)]×(m+2)2=
×[m﹣(﹣2)]×(m+2)2=![]() (m+2)3
(m+2)3
S梯形ONMB=![]() ON(MN+OB)
ON(MN+OB)
=![]() ×(﹣m)×[(m+2)2+4]
×(﹣m)×[(m+2)2+4]
=﹣![]() (m3+4m2+8m)
(m3+4m2+8m)
∴S△AMB=S△AOB﹣S△AMN﹣S梯形ONMB
=4﹣![]() (m+2)3﹣[﹣
(m+2)3﹣[﹣![]() (m3+4m2+8m)]
(m3+4m2+8m)]
=﹣m2﹣2m,当m=﹣1时,S△AMB最大,∵(﹣1+2)2=1
∴此时点M的坐标为(﹣1,1).
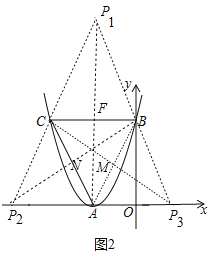
②存在.如图2中,∵四边形ABP1C是平行四边形,∴FC=FB,AF=FP1,∵B(0,4),C(﹣4,4),∴F(﹣2,4),设P1(x,y),则有![]() =﹣2,
=﹣2,![]() =4,∴x=﹣2,y=8,∴P1(﹣2,8),同法可得P2(﹣6,0),P3(2,0).
=4,∴x=﹣2,y=8,∴P1(﹣2,8),同法可得P2(﹣6,0),P3(2,0).
所有满足条件的点P的坐标是(2,0)、(﹣6,0)、(﹣2,8).
-
科目: 来源: 题型:
查看答案和解析>>【题目】小明用a小时清点完一批图书的一半,小强加入清点另一半图书的工作,两人合作
 小时清点完另一半图书.设小强单独清点完这批图书需要x小时.
小时清点完另一半图书.设小强单独清点完这批图书需要x小时.
(1)若a=3,求小强单独清点完这批图书需要的时间.
(2)请用含a的代数式表示x,并说明a满足什么条件时x的值符合实际意义. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知在△ABC中,AB=AC,射线BM、BN在∠ABC内部,分别交线段AC于点G、H.
(1)如图1,若∠ABC=60°、∠MBN=30°,作AE⊥BN于点D,分别交BC、BM于点E、F.
①求证:CE=AG;
②若BF=2AF,连接CF,求∠CFE的度数;
(2)如图2,点E为BC上一点,AE交BM于点F,连接CF,若∠BFE=∠BAC=2∠CFE,直接写出 的结果
的结果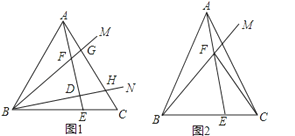
-
科目: 来源: 题型:
查看答案和解析>>【题目】分解因式:a3﹣4a= .
-
科目: 来源: 题型:
查看答案和解析>>【题目】某广告公司全体员工年薪的具体情况如表:
年薪/万元
25
15
10
6
4
人数
1
1
3
3
2
则该公司全体员工年薪的中位数是万元.
-
科目: 来源: 题型:
查看答案和解析>>【题目】明天下雨的概率为95%,那么下列说法错误的是( )
A. 明天下雨的可能性较大
B. 明天不下雨的可能性较小
C. 明天有可能是晴天
D. 明天不可能是晴天
-
科目: 来源: 题型:
查看答案和解析>>【题目】先化简,再求值:5x2﹣[4x2﹣(2x﹣1)﹣3x];其中x=3.
相关试题

