【题目】小明用a小时清点完一批图书的一半,小强加入清点另一半图书的工作,两人合作![]() 小时清点完另一半图书.设小强单独清点完这批图书需要x小时.
小时清点完另一半图书.设小强单独清点完这批图书需要x小时.
(1)若a=3,求小强单独清点完这批图书需要的时间.
(2)请用含a的代数式表示x,并说明a满足什么条件时x的值符合实际意义.
参考答案:
【答案】解:(1)设小强单独清点完这批图书需要x小时,由题意得:![]() +(
+(![]() +
+![]() )×
)×![]() =1,
=1,
解得:x=4,
经检验x=4是原分式方程的解.
答:小强单独清点完这批图书需要4小时.
(2)由题意得:![]() +(
+(![]() +
+![]() )×
)×![]() =1,
=1,
解得:x=![]() ,
,
a>![]() .
.
所以当a>![]() 时x的值符合实际意义.
时x的值符合实际意义.
【解析】(1)设小强单独清点这批图书需要的时间是x小时,根据“小明3小时清点完一批图书的一半”和“两人合作![]() 小时清点完另一半图书”列出方程,求出x的值,再进行检验,即可得出答案;
小时清点完另一半图书”列出方程,求出x的值,再进行检验,即可得出答案;
(2)根据小明完成的工作量加上两人合作完成的工作量为1,列出方程解答即可.
【考点精析】本题主要考查了分式方程的应用的相关知识点,需要掌握列分式方程解应用题的步骤:审题、设未知数、找相等关系列方程、解方程并验根、写出答案(要有单位)才能正确解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】若x2+y2=5,xy=2,求下列各式的值;
(1)(x+y)2(直接写出结果)
(2)x﹣y
(3) (直接写出结果)
(直接写出结果) -
科目: 来源: 题型:
查看答案和解析>>【题目】若﹣5x2ym与x2y是同类项,m= .
-
科目: 来源: 题型:
查看答案和解析>>【题目】化简:2(3a﹣2b)﹣3(a﹣3b)
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知在△ABC中,AB=AC,射线BM、BN在∠ABC内部,分别交线段AC于点G、H.
(1)如图1,若∠ABC=60°、∠MBN=30°,作AE⊥BN于点D,分别交BC、BM于点E、F.
①求证:CE=AG;
②若BF=2AF,连接CF,求∠CFE的度数;
(2)如图2,点E为BC上一点,AE交BM于点F,连接CF,若∠BFE=∠BAC=2∠CFE,直接写出 的结果
的结果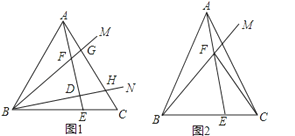
-
科目: 来源: 题型:
查看答案和解析>>【题目】分解因式:a3﹣4a= .
-
科目: 来源: 题型:
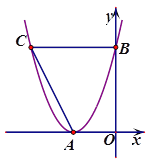
查看答案和解析>>【题目】如图,已知抛物线与x轴只有一个交点A(-2,0),与y轴交于点B(0,4).
(1)求抛物线对应的函数解析式;
(2)过点B做平行于x轴的直线交抛物线与点C.
①若点M在抛物线的AB段(不含A、B两点)上,求四边形BMAC面积最大时,点M的坐标;
②在平面直角坐标系内是否存在点P,使以P、A、B、C为顶点的四边形是平行四边形,若存在直接写出所有满足条件的点P的坐标;若不存在,请说明理由.
相关试题

