【题目】如图,O为直线AB上一点,OD平分∠AOC,∠DOE=90°.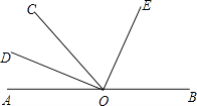
(1)请你数一数,图中有个小于平角的角;
(2)若∠AOC=50°,则∠COE的度数= , ∠BOE的度数=;
(3)猜想:OE是否平分∠BOC?请通过计算说明你猜想的结论.
参考答案:
【答案】
(1)9
(2)65°,65°
(3)解:结论:OE平分∠BOC.
理由:设∠AOC=2α,
∵OD平分∠AOC,∠AOC=2α,
∴∠AOD=∠COD= ![]() ∠AOC=α,
∠AOC=α,
又∵∠DOE=90°
∴∠COE=∠DOE﹣∠COD=90°﹣α.
又∵∠BOE=180°﹣∠DOE﹣∠AOD=180°﹣90°﹣α=90°﹣α,
∴∠COE=∠BOE,即OE平分∠BOC.
【解析】解:(1)∠AOD、∠COA、∠AOE、∠DOC、∠DOE、∠DOB、∠COE、∠COB、∠EOB共9个;
(2)∵OD平分∠AOC,
∴∠COD=∠AOD=![]() ∠AOC=50°,
∠AOC=50°,
∴∠COE=∠DOE-∠COD=90°-25°=65°,
∴∠BOE=180°-∠AOD-∠DOE=180°-25°-90°=65°.
(1)直接结合图形可写出所有的角;
(2)先角平分线的定义可求出∠COD、∠AOD的度数,再由∠COE=∠DOE-∠COD、∠BOE=180°-∠AOD-∠DOE可分别求出答案;
(3)设∠AOC=2α,利用平分线的定义可表示出∠AOD、∠COD,同(2)可表示出∠COE、∠BOE,进而可得答案.
-
科目: 来源: 题型:
查看答案和解析>>【题目】若多项式x2+mx-28可因式分解为(x-4)(x+7),则m的值为( )
A. -3 B. 11 C. -11 D. 3
-
科目: 来源: 题型:
查看答案和解析>>【题目】解方程:
(1)5(x﹣5)+2x=﹣4;
(2) =1﹣
=1﹣ 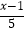 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】在等边三角形ABC的边BC上任取一点D,以CD为边向外作等边三角形CDE(如图①),连接AD,BE,易证明BE=AD.
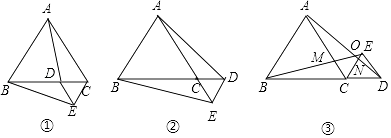
(1)若点D在射线BC上(如图②),其他条件均不变,BE=AD是否依然成立?试说明理由;
(2)在图②中,若等边三角形CDE与等边三角形ABC均在直线BC的同一侧(如图③),并且B,C,D三点在同一直线上,猜想BE=AD是否依然成立?试说明理由;
(3)在(2)的条件下,根据图汇总所标字母,请直接写出你发现的两个正确结论.
①;② . -
科目: 来源: 题型:
查看答案和解析>>【题目】一元二次方程x2﹣4x+2=0的根的情况是( )
A.有两个不相等的实数根
B.有两个相等的实数根
C.只有一个实数根
D.没有实数根 -
科目: 来源: 题型:
查看答案和解析>>【题目】小刚在A,B两家体育用品商店都发现了他看中的羽毛球拍和篮球,两家商店的羽毛球拍和篮球的单价都是相同的,羽毛球拍和篮球单价之和是426元,且篮球的单价是羽毛球拍的单价的4倍少9元.
(1)求小刚看中的羽毛球拍和篮球的单价各是多少元?
(2)小刚在元旦这一天上街,恰好赶上商店促销,A商店所有商品打八五折销售,B商店全场购物满100元返购物券20元(不足100元不返券,购物券全场通用,用购物券购物不再返券),但他只带了380元钱,如果他只在一家商店购买看中的这两样商品,你能说明他可以选择在哪一家购买吗?若两家都可以选择,在哪一家购买更省钱? -
科目: 来源: 题型:
查看答案和解析>>【题目】一个正方形的面积为x2+4x+4(x>0),则它的边长为________.
相关试题

