【题目】如图,在△ABC中,CD⊥AB于点D,AC=4,BC=3,DB=![]() ,
,
(1)求CD、AD的长
(2)判断△ABC的形状,并说明理由。

参考答案:
【答案】(1)、CD=![]() ,AD=
,AD=![]() ;(2)、直角三角形,理由见解析
;(2)、直角三角形,理由见解析
【解析】
试题分析:(1)、根据CD⊥AB,BC=3,BD=![]() 得出△CDB和△ADC为直角三角形,然后根据直角三角形的勾股定理分别求出CD和AD的长度;(2)、根据题意得出AC,BC和AB的长度,然后根据勾股定理的逆定理得出三角形为直角三角形.
得出△CDB和△ADC为直角三角形,然后根据直角三角形的勾股定理分别求出CD和AD的长度;(2)、根据题意得出AC,BC和AB的长度,然后根据勾股定理的逆定理得出三角形为直角三角形.
试题解析:(1)、∵CD⊥AB,BC=3,BD=![]() ∴∠CDB=∠CDA=90° ∴在Rt△CDB中,由勾股定理可得:
∴∠CDB=∠CDA=90° ∴在Rt△CDB中,由勾股定理可得:
CD=![]()
在Rt△ADC中,AC=4,CD=![]() ,由勾股定理可得:AD=
,由勾股定理可得:AD=![]()
(2)、△ABC为直角三角形
∵在△ABC中,AC=4,BC=3,AB=AD+BD=![]() +
+![]() =5 ∴
=5 ∴![]()
∴由勾股定理的逆定理可得:△ABC为直角三角形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】两个大小不同的等腰直角三角形三角板如图
 所示放置,图
所示放置,图 是由它抽象出的几何图形,B,C,E在同一条直线上,联结DC,
是由它抽象出的几何图形,B,C,E在同一条直线上,联结DC, 请找出图
请找出图 中的全等三角形,并给予说明
中的全等三角形,并给予说明 说明:结论中不得含有未标识的字母
说明:结论中不得含有未标识的字母 ;
; 试说明:
试说明: .
.
-
科目: 来源: 题型:
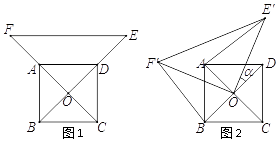
查看答案和解析>>【题目】如图1,已知
 为正方形
为正方形  的中心,分别延长
的中心,分别延长  到点
到点  ,
,  到点
到点  ,使
,使  ,
,  ,连结
,连结 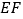 ,将△
,将△  绕点
绕点  逆时针旋转
逆时针旋转  角得到△
角得到△ 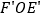 (如图2).连结
(如图2).连结  、
、  .
.
(Ⅰ)探究 与
与  的数量关系,并给予证明;
的数量关系,并给予证明;
(Ⅱ)当 ,
,  时,求:
时,求:
① 的度数;
的度数;
② 的长度.
的长度. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,抛物线
 与
与 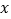 轴交于
轴交于  、
、  两点(点
两点(点  在点
在点  的左侧),点
的左侧),点  的坐标为
的坐标为  ,与
,与  轴交于点
轴交于点  ,作直线
,作直线  .动点
.动点  在
在 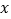 轴上运动,过点
轴上运动,过点  作
作  轴,交抛物线于点
轴,交抛物线于点  ,交直线
,交直线  于点
于点  ,设点
,设点  的横坐标为
的横坐标为 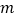 .
.
(Ⅰ)求抛物线的解析式和直线 的解析式;
的解析式;
(Ⅱ)当点 在线段
在线段  上运动时,求线段
上运动时,求线段  的最大值;
的最大值;
(Ⅲ)当以 、
、 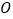 、
、  、
、  为顶点的四边形是平行四边形时,直接写出
为顶点的四边形是平行四边形时,直接写出 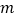 的值.
的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(列二元一次方程组解应用题)某公司共有3个一样规模的大餐厅和2个一样规模的小餐厅,经过测试同时开放2个大餐厅和1个小餐厅,可供300名员工就餐;同时开放1个大餐厅,1个小餐厅,可供170名员工就餐.
(1)请问1个大餐厅、1个小餐厅分别可供多少名员工就餐;
(2)如果3个大餐厅和2个小餐厅全部开放,那么能否供全体450名员工就餐?请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)如图1,AB∥CD,∠A=38°,∠C=50°,求∠APC的度数.(提示:作PE∥AB).
(2)如图2,AB∥DC,当点P在线段BD上运动时,∠BAP=∠α,∠DCP=∠β,求∠CPA与∠α,∠β之间的数量关系,并说明理由.
(3)在(2)的条件下,如果点P在段线OB上运动,请你直接写出∠CPA与∠α,∠β之间的数量关系______.

-
科目: 来源: 题型:
查看答案和解析>>【题目】通过对某校七年级学生体育选修课程的统计,得到以下信息:
①参加选课的总人数为300;
②参加选课的学生在“足球、篮球、排球、乒乓球”中都选择了一门;
③选足球和选排球的人数共占总人数的50%;选乒乓球的人数是选排球人数的2倍;
选足球和选篮球的人数共占总人数的85%.
设选足球的人数为x,选排球的人数为y,试列出二元一次方程组,分别求出选择足球、篮球、排球、乒乓球各门课程的人数.
相关试题

