搜索
【题目】如图，将矩形ABCD沿CE向上折叠，使点B落在AD边上的点F处．若AE=
BE，则长AD与宽AB的比值是 ．
参考答案：
【答案】
．
【解析】
试题分析：∵AE=
BE，∴设AE=2k，则BE=3k，AB=5k．
∵四边形ABCD是矩形，∴∠A=∠ABC=∠D=90°，CD=AB=5k，AD=BC．
∵将矩形ABCD沿CE向上折叠，使点B落在AD边上的点F处，∴∠EFC=∠B=90°，EF=EB=3k，CF=BC，∴∠AFE+∠DFC=90°，∠DFC+∠FCD=90°，∴∠DCF=∠AFE，∴cos∠AFE=cos∠DCF．
在Rt△AEF中，∵∠A=90°，AE=2k，EF=3k，∴AF=
=
，∴
，即
，∴CF=
，∴AD=BC=CF=，∴长AD与宽AB的比值是
=．
故答案为：．
-
科目： 来源： 题型：
查看答案和解析>>【题目】用一个平面去截一个正方体，截面的形状可能是（ ）
A. 六边形 B. 七边形 C. 八边形 D. 九边形
-
科目： 来源： 题型：
查看答案和解析>>【题目】用科学记数法表示数5230000，结果正确的是( )
A. 523×104 B. 5.23×104 C. 52.3×105 D. 5.23×106
-
科目： 来源： 题型：
查看答案和解析>>【题目】大于 -2.6且小于4的整数有 （ ）
A. 4个 B. 5个 C. 6个 D. 7个
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在矩形OABC中，点O为原点，点A的坐标为（0，8），点C的坐标为（6，0）．抛物线
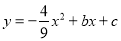经过点A、C，与AB交于点D．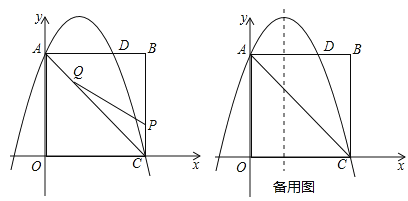
（1）求抛物线的函数解析式；
（2）点P为线段BC上一个动点（不与点C重合），点Q为线段AC上一个动点，AQ=CP，连接PQ，设CP=m，△CPQ的面积为S．
①求S关于m的函数表达式；
②当S最大时，在抛物线
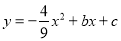的对称轴l上，若存在点F，使△DFQ为直角三角形，请直接写出所有符合条件的点F的坐标；若不存在，请说明理由． -
科目： 来源： 题型：
查看答案和解析>>【题目】写出“同位角相等，两直线平行”的题设为 ， 结论为 ．
-
科目： 来源： 题型：
查看答案和解析>>【题目】某种品牌的手机经过四、五月份连续两次降价，每部售价由3200元降到了2500元．设平均每月降价的百分率为x，根据题意列出的方程是（ ）
A. 2500(1＋x)2＝3200 B. 2500(1＋2x)＝3200
C. 3200(1－x)2＝2500 D. 3200(1－2x)＝2500
相关试题
