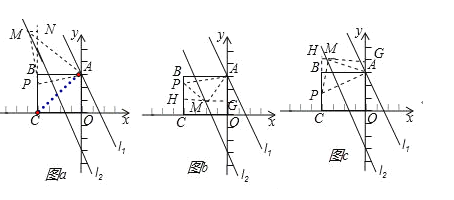
【题目】如图,在矩形ABCO中,点O为坐标原点,点B的坐标为(﹣4,3),点A,C在坐标轴上,将直线l1:y=﹣2x+3向下平移6个单位长度得到直线l2.
(1)求直线l2的解析式;
(2)求直线l2与两坐标轴围成的三角形的面积S;
(3)已知点M在第二象限,且是直线l2上的点,点P在BC边上,若△APM是等腰直角三角形,求点M的坐标.

参考答案:
【答案】(1)y=﹣2x﹣3;(2)![]() ;(3)点M的坐标为(﹣
;(3)点M的坐标为(﹣![]() ,
,![]() )或(﹣2,1)或(﹣
)或(﹣2,1)或(﹣![]() ,
,![]() ).
).
【解析】
(1)根据平移规律得出直线l2的解析式即可;
(2)根据坐标轴上点的坐标特征可求直线l1与x轴,直线l2与AB的交点坐标;
(3)分三种情况:①若点A为直角顶点时,点M在第二象限;若点P为直角顶点时,点M在第二象限;③若点M为直角顶点时,点M在第二象限;进行讨论可求点M的坐标;
解:(1)直线l2的解析式为y=﹣2x+3﹣6=﹣2x﹣3.
(2)由(1)知直线l2的解析式为y=﹣2x﹣3,令y=0,即﹣2x﹣3=0,
∴x=﹣![]() ;
;
令x=0,则y=﹣3,
∴S=![]() ×3×
×3×![]() =
=![]() .
.
(3)若△APM是等腰直角三角形,分以下三种情况讨论:①当点A为直角顶点时,∠MPA=45°,连接AC,如图a.
∵点M在第二象限,若∠MAP=90°,则点M必在AB上方,
∴∠MPA>∠BPA>∠BCA=45°,这与∠MPA=45°矛盾,
∴点M不存在;
②当点P为直角顶点时,即∠MPA=90°.
∵M在第二象限,
∴点M必在AB上方,如图a,过点M作MN⊥CB交CB的延长线于点N,易证△ABP≌△PNM,
∴PN=AB=4,MN=BP.
∵B(﹣4,3),
∴CB=3.设点M的坐标为(x,﹣2x﹣3),则BP=MN=﹣4﹣x,CN=﹣2x﹣3.
∵CN=CB+PN﹣BP,
∴﹣2x﹣3=3+4﹣(﹣4﹣x),
∴x=﹣![]() ,则﹣2x﹣3=
,则﹣2x﹣3=![]() ,
,
∴点M的坐标为(﹣![]() ,
,![]() );
);
③当点M为直角顶点时,分两种情况讨论:如图b,当点M在AB下方时,过点M作HG⊥OA交OA于点G,交BC于点H,易证△MPH≌△AMG,
∴MH=AG.设点M的坐标为(a,﹣2a﹣3),则AG=3﹣(﹣2a﹣3)=6+2a,MG=﹣a,
∴HG=MH+MG=AG+MG=6+2a﹣a=4,
∴a=﹣2,则﹣2a﹣3=1.
∴点M的坐标为(﹣2,1);
如图c,当点M在AB上方时,同理可得﹣2a﹣6﹣a=4,
∴a=﹣![]() ,则﹣2a﹣3=
,则﹣2a﹣3=![]() ,
,
∴点M2的坐标为(﹣![]() ,
,![]() ),
),
综上所述,点M的坐标为(﹣![]() ,
,![]() )或(﹣2,1)或(﹣
)或(﹣2,1)或(﹣![]() ,
,![]() ).
).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AB=AC,AD平分∠BAC,CE∥AD且CE=AD.
(1)求证:四边形ADCE是矩形;
(2)若△ABC是边长为
 的等边三角形,AC,DE相交于点O,在CE上截取CF=CO,连接OF,求线段FC的长及四边形AOFE的面积.
的等边三角形,AC,DE相交于点O,在CE上截取CF=CO,连接OF,求线段FC的长及四边形AOFE的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下面是“作已知角的角平分线”的尺规作图过程.
已知:如图1,∠MON.


求作:射线OP,使它平分∠MON.
作法:如图2,
(1)以点O为圆心,任意长为半径作弧,交OM于点A,交ON于点B;
(2)连结AB;
(3)分别以点A,B为圆心,大于
 AB的长为半径作弧,两弧相交于点P;
AB的长为半径作弧,两弧相交于点P;(4)作射线OP.
所以,射线OP即为所求作的射线.
请回答:该尺规作图的依据是______.
-
科目: 来源: 题型:
查看答案和解析>>【题目】观察如图所示的图形,回答下列问题:
(1)按甲方式将桌子拼在一起.
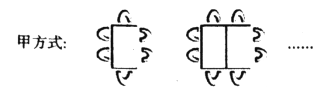
4张桌子拼在一起共有 个座位,n张桌子拼在一起共有 个座位;
(2)按乙方式将桌子拼在一起.
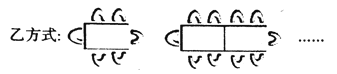
6张桌子拼在一起共有 个座位,m张桌子拼在一起共有 个座位;
(3)某食堂有A,B两个餐厅,现有102张这样的长方形桌子,计划把这些桌子全放在两个餐厅,每个餐厅都要放有桌子.将a张桌子放在A餐厅,按甲方式每6张拼成1张大桌子;将其余桌子都放在B餐厅,按乙方式每4张桌子拼成1张大桌子,若两个餐厅一共有404个座位,问A,B两个餐厅各有多少个座位?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在□ABCD中,BF平分∠ABC交AD于点F,AE⊥BF于点O,交BC于点E,连接EF.
(1)求证:四边形ABEF是菱形;
(2)连接CF,若∠ABC=60°,AB= 4,AF =2DF,求CF的长.

-
科目: 来源: 题型:
查看答案和解析>>【题目】为了解某区初二年级数学学科期末质量监控情况,进行了抽样调查,过程如下,请将有关问题补充完整.
收集数据:随机抽取甲乙两所学校的20名学生的数学成绩进行分析:
甲
91
89
77
86
71
31
97
93
72
91
81
92
85
85
95
88
88
90
44
91
乙
84
93
66
69
76
87
77
82
85
88
90
88
67
88
91
96
68
97
59
88
整理、描述数据:按如下数据段整理、描述这两组数据
分段
学校
30≤x≤39
40≤x≤49
50≤x≤59
60≤x≤69
70≤x≤79
80≤x≤89
90≤x≤100
甲
1
1
0
0
3
7
8
乙
分析数据:两组数据的平均数、中位数、众数、方差如下表:
统计量
学校
平均数
中位数
众数
方差
甲
81.85
88
91
268.43
乙
81.95
86
m
115.25
经统计,表格中m的值是 .
得出结论:
a若甲学校有400名初二学生,估计这次考试成绩80分以上人数为 .
b可以推断出 学校学生的数学水平较高,理由为 .(至少从两个不同的角度说明推断的合理性)
-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读材料:若
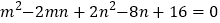 ,求m、n的值.
,求m、n的值.解:
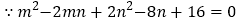 ,
,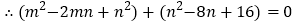
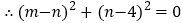 ,
,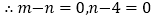 ,
, 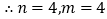 .
.根据你的观察,探究下面的问题:
(1)己知
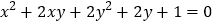 ,求
,求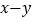 的值.
的值.(2)已知△ABC的三边长a、b、c都是正整数,且满足
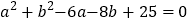 ,求边c的最大值.
,求边c的最大值.(3) 若己知
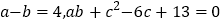 ,求
,求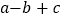 的值.
的值.
相关试题

