【题目】下面是“作已知角的角平分线”的尺规作图过程.
已知:如图1,∠MON.


求作:射线OP,使它平分∠MON.
作法:如图2,
(1)以点O为圆心,任意长为半径作弧,交OM于点A,交ON于点B;
(2)连结AB;
(3)分别以点A,B为圆心,大于![]() AB的长为半径作弧,两弧相交于点P;
AB的长为半径作弧,两弧相交于点P;
(4)作射线OP.
所以,射线OP即为所求作的射线.
请回答:该尺规作图的依据是______.
参考答案:
【答案】答案不唯一:到线段两端点距离相等的点在线段的垂直平分线上;等腰三角形三线合一.
【解析】分析:在作法中通过线段的垂直平分线的判定定理或等腰三角形的三线合一的性质,结合全等即可证明出所作的射线OP平分∠MON.
详解:如图所示,

∵由尺规作图可知,
OA=OB,PA=PB,
∴OP垂直且平分AB,
∴∠OEA=∠OEB=90°,AE=BE,
又∵OE=OE,
∴△OEA≌△∠OEB,
∴∠AOE=∠BOE,
∴所作的射线OP平分∠MON.
故答案为:到线段两端点距离相等的点在线段的垂直平分线上或等腰三角形三线合一.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某汽车运输公司根据实际需要计划购买大、中型两种客车共20辆,已知大型客车每辆62万元,中型客车每辆40万元,设购买大型客车x(辆),购车总费用为y(万元).
(1)求y与x的函数关系式(不要求写出自变量x的取值范围);
(2)若购买中型客车的数量少于大型客车的数量,请你给出一种费用最省的方案,并求出该方案所需费用.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知抛物线
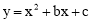 的图象与x轴的一个交点为B(5,0),另一个交点为A,且与y轴交于点C(0,5)。
的图象与x轴的一个交点为B(5,0),另一个交点为A,且与y轴交于点C(0,5)。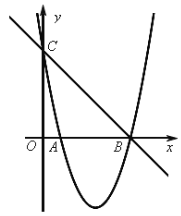
(1)求直线BC与抛物线的解析式;
(2)若点M是抛物线在x轴下方图象上的动点,过点M作MN∥y轴交直线BC于点N,求MN的最大值;
(3)在(2)的条件下,MN取得最大值时,若点P是抛物线在x轴下方图象上任意一点,以BC为边作平行四边形CBPQ,设平行四边形CBPQ的面积为S1,△ABN的面积为S2,且S1=6S2,求点P的坐标。
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AB=AC,AD平分∠BAC,CE∥AD且CE=AD.
(1)求证:四边形ADCE是矩形;
(2)若△ABC是边长为
 的等边三角形,AC,DE相交于点O,在CE上截取CF=CO,连接OF,求线段FC的长及四边形AOFE的面积.
的等边三角形,AC,DE相交于点O,在CE上截取CF=CO,连接OF,求线段FC的长及四边形AOFE的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】观察如图所示的图形,回答下列问题:
(1)按甲方式将桌子拼在一起.
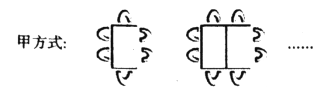
4张桌子拼在一起共有 个座位,n张桌子拼在一起共有 个座位;
(2)按乙方式将桌子拼在一起.
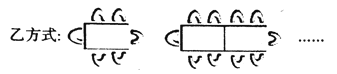
6张桌子拼在一起共有 个座位,m张桌子拼在一起共有 个座位;
(3)某食堂有A,B两个餐厅,现有102张这样的长方形桌子,计划把这些桌子全放在两个餐厅,每个餐厅都要放有桌子.将a张桌子放在A餐厅,按甲方式每6张拼成1张大桌子;将其余桌子都放在B餐厅,按乙方式每4张桌子拼成1张大桌子,若两个餐厅一共有404个座位,问A,B两个餐厅各有多少个座位?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在矩形ABCO中,点O为坐标原点,点B的坐标为(﹣4,3),点A,C在坐标轴上,将直线l1:y=﹣2x+3向下平移6个单位长度得到直线l2.
(1)求直线l2的解析式;
(2)求直线l2与两坐标轴围成的三角形的面积S;
(3)已知点M在第二象限,且是直线l2上的点,点P在BC边上,若△APM是等腰直角三角形,求点M的坐标.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在□ABCD中,BF平分∠ABC交AD于点F,AE⊥BF于点O,交BC于点E,连接EF.
(1)求证:四边形ABEF是菱形;
(2)连接CF,若∠ABC=60°,AB= 4,AF =2DF,求CF的长.

相关试题

