【题目】已知正方形ABCD和等腰Rt△BEF,BE=EF,∠BEF=90°,按图放置,使点E在BC上,取DF的中点G,连结EG、CG.
(1)请添加一条辅助线,构造一个和△FEG全等的三角形,并证明它们全等.
(2)探索EG、CG的数量关系和位置关系,并证明.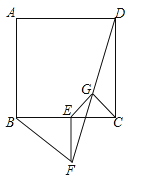
参考答案:
【答案】解:(1)延长EG交CD于点H,如图,则△DHG≌△FEG.证明如下:
∵∠BEF=90°,
∴EF⊥BC,
而CD⊥BC,
∴EF∥CD,
∴∠1=∠2,
∵点G为DF的中点,
∴DG=FG,
在△DHG和△FEG中,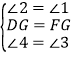 ,
,
∴△DHG≌△FEG(ASA);
(2)EG=CG,EG⊥CG.证明如下:
∵△DHG≌△FEG,
∴EF=DH,EG=HG,
∵BE=EF,
∴BE=DH,
∵CB=CD,
∴CD﹣DH=CB﹣BE,即CH=CE,
∴△CHE为等腰直角三角形,
∵EG=GH,
∴CG⊥EH,CG=EG=GH,
即EG=CG,EG⊥CG.
【解析】(1)延长EG交CD于点H,如图,先证明EF∥CD,则∠1=∠2,再由点G为DF的中点得到DG=FG,然后利用“ASA”判断△DHG≌△FEG;
(2)由△DHG≌△FEG得到EF=DH,EG=HG,而BE=EF,所以BE=DH,根据正方形的性质得CB=CD,则CH=CE,于是可判断△CHE为等腰直角三角形,然后根据等腰直角三角形的性质得到CG⊥EH,CG=EG=GH,即EG=CG,EG⊥CG.
【考点精析】解答此题的关键在于理解正方形的性质的相关知识,掌握正方形四个角都是直角,四条边都相等;正方形的两条对角线相等,并且互相垂直平分,每条对角线平分一组对角;正方形的一条对角线把正方形分成两个全等的等腰直角三角形;正方形的对角线与边的夹角是45o;正方形的两条对角线把这个正方形分成四个全等的等腰直角三角形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)如图1,4条直线l1、l2、l3、l4是一组平行线,相邻2条平行线的距离都是2cm,正方形ABCD的4个顶点A、B、C、D分别在l1、l3、l4、l2上,求该正方形的面积;
(2)如图2,把一张矩形卡片ABCD放在每格宽度为18mm的横格纸中,恰好四个顶点都在横格线上,已知∠1=36°,求长方形卡片的周长.(精确到1mm)(参考数据:sin36°≈0.60,cos36°≈0.80,tan36°≈0.75)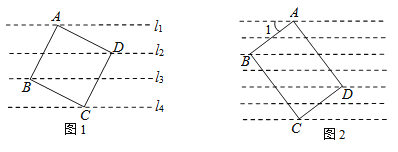
-
科目: 来源: 题型:
查看答案和解析>>【题目】若代数式(4x2-mx-3y+4)-(8nx2-x+2y-3)的值与字母x的取值无关,求代数式(-m2+2mn-n2)-2(mn-3m2)+3(2n2-mn)的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】用三角形和六边形按如图所示的规律拼图案.

(1)第4个图案中,三角形的个数有________个,六边形的个数有________个;
(2)第n(n为正整数)个图案中,三角形的个数与六边形的个数各有多少个?
(3)第2017个图案中,三角形的个数与六边形的个数各有多少个?
(4)是否存在某个符合上述规律的图案,其中有100个三角形与30个六边形?如果有,指出是第几个图案;如果没有,说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】若多项式-6ab+18abx+24aby的一个因式是-6ab,那么另一个因式是
A. 1-3x-4y B. -1-3x-4y
C. 1+3x-4y D. -1-3x+4y
-
科目: 来源: 题型:
查看答案和解析>>【题目】2x﹣5y+3x+y﹣2
-
科目: 来源: 题型:
查看答案和解析>>【题目】若x﹣2y=4,则(2y﹣x)2+2x﹣4y+1的值是_____.
相关试题

