【题目】根据《广州市初中学业水平考试体育与健康考试实施意见(征求意见稿)》,![]() 年的广州市体育中考将要求考生在足球、排球、篮球三个项目中任选一项参加考试.某校数学兴趣小组的同学为了解本校初一学生对足球、排球、篮球这三大球类运动项目的选考情况,抽取了部分学生进行调查,并根据调查结果绘制了两幅不完整的统计图,请你根据图中信息解答下列问题:
年的广州市体育中考将要求考生在足球、排球、篮球三个项目中任选一项参加考试.某校数学兴趣小组的同学为了解本校初一学生对足球、排球、篮球这三大球类运动项目的选考情况,抽取了部分学生进行调查,并根据调查结果绘制了两幅不完整的统计图,请你根据图中信息解答下列问题:
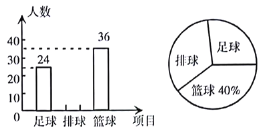
(1)求此次抽样调查的样本容量;
(2)补全条形统计图,并求扇形统计图中“足球”部分的圆心角度数;
(3)如果这所学校初一学生共![]() 人,请你估计该校初一有多少名学生选择排球项目参加体育中考?
人,请你估计该校初一有多少名学生选择排球项目参加体育中考?
参考答案:
【答案】(1)90;(2)见解析;![]() ;(3)115.
;(3)115.
【解析】
(1)由统计图获得信息,篮球项目选考人数和所占比例均已知,便可求得总体,即可得出样本容量;
(2)总体得知后,则可求出排球选考人数,足球选考人数所占比例,即可补齐条形统计图,并求得扇形统计图中“足球”部分的圆心角度数;
(3)首先求出排球选考所占比例,即可估计该校选择排球项目参加体育中考的人数.
解:(1)由统计图信息,可得篮球项目选考人数是36,所占![]() ,则
,则
所调查总体为![]() ,
,
即样本容量为90;
(2)根据(1)中信息总体人数是90,足球选考人数是24,篮球选考人数是36,则
排球选考人数是![]() ,
,
补齐的条形统计图,如图所示:
足球选考人数所占比例为![]() ,
,
其所对圆心角的度数为![]() ;
;
(3)由(1)中得知,排球选考人数占总数的![]() ,则有
,则有
![]() (人)
(人)
答:该校初一有115名学生选择排球项目参加体育中考.
-
科目: 来源: 题型:
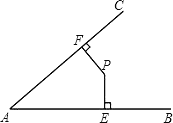
查看答案和解析>>【题目】如图所示,P是∠BAC内的一点,PE⊥AB,PF⊥AC,垂足分别为点E,F,AE=AF.求证:
(1)PE=PF;
(2)点P在∠BAC的平分线上.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,反比例函数y=
 与一次函数y=ax+b交于A(3,1)和B(1,m)两点.
与一次函数y=ax+b交于A(3,1)和B(1,m)两点.
(1)求一次函数和反比例函数的解析式;
(2)结合函数图象,请直接写出
 >ax+b的解集;
>ax+b的解集;(3)若P是x轴上一点,且△ABP的面积是6,求点P的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】列方程解应用题:某玩具厂生产一种玩具,按照控制固定成本降价促销的原则,使生产的玩具能够及时售出,据市场调查:每个玩具按480元销售时,每天可销售160个;若销售单价每降低1元,每天可多售出2个,已知每个玩具的固定成本为360元,问这种玩具的销售单价为多少元时,厂家每天可获利润最多?最多获利是多少元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】小明根据学习函数的经验,对函数
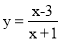 的图像与性质进行了探究.请补充完整:
的图像与性质进行了探究.请补充完整:(1)先填表,再在如图所示的平面直角坐标系中,描全表中各对对应值为坐标的点,并画出该函数的图像:
x
…
-5
-4
-3
-2
0
1
2
3
…
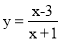
…
2
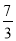
3
-3
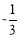
0
…
(2)结合函数的图像,说出两条不同类型的性质;
①________________________________;____________________________________.
②
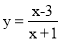 的图像是由
的图像是由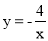 的图像如何平移得到?
的图像如何平移得到?___________________________________________.
(3)当函数值
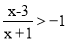 时,x的取值范围是____________span>.
时,x的取值范围是____________span>.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中有Rt△ABC,∠BAC=90°,AB=AC,A(3,0),B(0,1)

(1)将△ABC沿x轴的正方向平移t个单位,B、C两点的对应点B′、C′正好落在反比例函数y=
 的图象上.请直接写出C点的坐标和t,k的值;
的图象上.请直接写出C点的坐标和t,k的值;(2)有一个Rt△DEF,∠D=90°,∠E=60°,DE=2,将它放在直角坐标系中,使斜边EF在x轴上,直角顶点D在(1)中的反比例函数图象上,求点F的坐标;
(3)在(1)的条件下,问是否存在x轴上的点M和反比例函数y=
 图象上的点N,使得以B′、C′、M、N为顶点的四边形构成平行四边形?如果存在,直接写出所有满足条件的点M和点N的坐标;如果不存在,请说明理由.
图象上的点N,使得以B′、C′、M、N为顶点的四边形构成平行四边形?如果存在,直接写出所有满足条件的点M和点N的坐标;如果不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】学校计划组织
 名师生租乘汽车外出研学一天,需租用大巴、中巴共
名师生租乘汽车外出研学一天,需租用大巴、中巴共 辆,且要求租用的车子不留空位也不超载,大巴每辆可乘坐
辆,且要求租用的车子不留空位也不超载,大巴每辆可乘坐 名乘客,中巴每辆可乘坐
名乘客,中巴每辆可乘坐 名乘客.
名乘客.(1)求该校应租用大巴、中巴各多少辆?(请用含
 的代数式表示)
的代数式表示)(2)若每辆大巴租金是
 元/天,中巴租金是
元/天,中巴租金是 元/天,若租金不能超过
元/天,若租金不能超过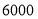 元,则应租用大巴、中巴各多少辆?
元,则应租用大巴、中巴各多少辆?
相关试题

