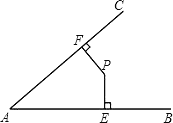
【题目】如图所示,P是∠BAC内的一点,PE⊥AB,PF⊥AC,垂足分别为点E,F,AE=AF.求证:
(1)PE=PF;
(2)点P在∠BAC的平分线上.
参考答案:
【答案】(1)见解析;(2)见解析.
【解析】
(1)连接AP,根据HL证明△APF≌△APE,可得到PE=PF;(2)利用(1)中的全等,可得出∠FAP=∠EAP,那么点P在∠BAC的平分线上.
证明:(1)如图,连接AP并延长,
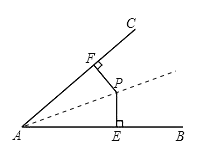
∵PE⊥AB,PF⊥AC,
∴∠AEP=∠AFP=90°,
又AE=AF,AP=AP,
∵在Rt△AFP和Rt△AEP中
![]() ,
,
∴Rt△AEP≌Rt△AFP(HL),
∴PE=PF.
(2)∵Rt△AEP≌Rt△AFP,
∴∠EAP=∠FAP,
∴AP是∠BAC的角平分线,故点P在∠BAC的角平分线上.
-
科目: 来源: 题型:
查看答案和解析>>【题目】自2020年开始,新冠病毒疫情严峻,某爱心组织紧急筹集了部分资金,计划购买甲、乙两种救灾物品共4000件送往武汉,已知每件甲种物品的价格比每件乙种物品的价格贵10元,用450元购买甲种物品的件数恰好与用400元购买乙种物品的件数相同.
(1)求甲、乙两种救灾物品每件的价格分别是多少元?
(2)经调查,灾区对乙种物品件数需求量是甲种物品件数的3倍,若该爱心组织按照此需求的比例购买这4000件物品,需筹集资金多少元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】(阅读理解)
在解方程组或求代数式的值时,可以用整体代入或整体求值的方法,化难为易.
(1)解方程组
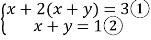
(2)已知
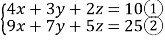 ,求x+y+z的值
,求x+y+z的值解:(1)把②代入①得:x+2×1=3.解得:x=1.
把x=1代入②得:y=0.
所以方程组的解为
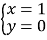 ,
,(2)①×2得:8x+6y+4z=20.③
②﹣③得:x+y+z=5.
(类比迁移)
(1)若
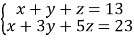 ,则x+2y+3z= .
,则x+2y+3z= .(2)解方程组
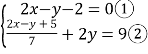
(实际应用)
打折前,买39件A商品,21件B商品用了1080元.打折后,买52件A商品,28件B商品用了1152元,比不打折少花了多少钱?
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,在△ABC、△ADE中,∠BAC=∠DAE=90°,AB=AC,AD=AE,点C、D、E三点在同一直线上,连结BD.求证:
(1)△BAD≌△CAE;
(2)BD⊥CE

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,反比例函数y=
 与一次函数y=ax+b交于A(3,1)和B(1,m)两点.
与一次函数y=ax+b交于A(3,1)和B(1,m)两点.
(1)求一次函数和反比例函数的解析式;
(2)结合函数图象,请直接写出
 >ax+b的解集;
>ax+b的解集;(3)若P是x轴上一点,且△ABP的面积是6,求点P的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】列方程解应用题:某玩具厂生产一种玩具,按照控制固定成本降价促销的原则,使生产的玩具能够及时售出,据市场调查:每个玩具按480元销售时,每天可销售160个;若销售单价每降低1元,每天可多售出2个,已知每个玩具的固定成本为360元,问这种玩具的销售单价为多少元时,厂家每天可获利润最多?最多获利是多少元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】根据《广州市初中学业水平考试体育与健康考试实施意见(征求意见稿)》,
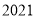 年的广州市体育中考将要求考生在足球、排球、篮球三个项目中任选一项参加考试.某校数学兴趣小组的同学为了解本校初一学生对足球、排球、篮球这三大球类运动项目的选考情况,抽取了部分学生进行调查,并根据调查结果绘制了两幅不完整的统计图,请你根据图中信息解答下列问题:
年的广州市体育中考将要求考生在足球、排球、篮球三个项目中任选一项参加考试.某校数学兴趣小组的同学为了解本校初一学生对足球、排球、篮球这三大球类运动项目的选考情况,抽取了部分学生进行调查,并根据调查结果绘制了两幅不完整的统计图,请你根据图中信息解答下列问题: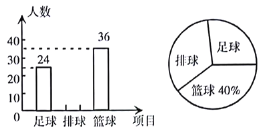
(1)求此次抽样调查的样本容量;
(2)补全条形统计图,并求扇形统计图中“足球”部分的圆心角度数;
(3)如果这所学校初一学生共
 人,请你估计该校初一有多少名学生选择排球项目参加体育中考?
人,请你估计该校初一有多少名学生选择排球项目参加体育中考?
相关试题

