【题目】如图,在平行四边形ABCD中,∠DAB=60°,AB=2AD,点 E、F分别是AB、CD的中点,过点A作AG∥BD,交CB的延长线于点G. 
(1)求证:四边形DEBF是菱形;
(2)请判断四边形AGBD是什么特殊四边形?并加以证明.
参考答案:
【答案】
(1)证明:∵四边形ABCD是平行四边形
∴AB∥CD且AB=CD,AD∥BC且AD=BC
E,F分别为AB,CD的中点,
∴BE= ![]() AB,DF=
AB,DF= ![]() CD,
CD,
∴BE=DF,
∴四边形DEBF是平行四边形
在△ABD中,E是AB的中点,
∴AE=BE= ![]() AB=AD,
AB=AD,
而∠DAB=60°
∴△AED是等边三角形,即DE=AE=AD,
故DE=BE
∴平行四边形DEBF是菱形
(2)解:四边形AGBD是矩形,理由如下:
∵AD∥BC且AG∥DB
∴四边形AGBD是平行四边形
由(1)的证明知AD=DE=AE=BE,
∴∠ADE=∠DEA=60°,
∠EDB=∠DBE=30°
故∠ADB=90°
∴平行四边形AGBD是矩形.
【解析】(1)利用平行四边形的性质证得△AED是等边三角形,从而证得DE=BE,问题得证;(2)利用平行四边形的性质证得∠ADB=90°,利用有一个角是直角的平行四边形是矩形判定矩形.
【考点精析】本题主要考查了三角形中位线定理和平行四边形的性质的相关知识点,需要掌握连接三角形两边中点的线段叫做三角形的中位线;三角形中位线定理:三角形的中位线平行于三角形的第三边,且等于第三边的一半;平行四边形的对边相等且平行;平行四边形的对角相等,邻角互补;平行四边形的对角线互相平分才能正确解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,BD是∠ABC的角平分线,DE∥BC,交AB于点E,∠A=45°, ∠BDC=60°。
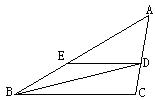
(1)求∠C的度数;
(2)求∠BED的度数. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知不论x为何值,x2-kx-15=(x+5)(x-3),则k值为( )
A. 2 B. -2 C. 5 D. -3
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列关系一定成立的是( )
A. 若|a|=|b|,则a=b B. 若|a|=b,则a=b
C. 若|a|=﹣b,则a=b D. 若a=﹣b,则|a|=|b|
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在ABCD中,∠BAD的平分线交BC于点E,∠BCD的平分线交AD于点F.

(1)求证:四边形AECF是平行四边形;
(2)若AE=5,BC﹣AB=3,求四边形AECF的周长. -
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,将点A(﹣2,3)向右平移a个单位长度,再向下平移b个单位长度,平移后对应的点为A′,且点A和A′关于原点对称,则a+b=_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】探究与发现:
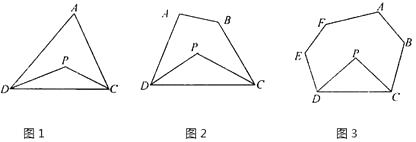
(1)探究一:三角形的一个内角与另两个内角的平分线所夹的角之间的关系
已知:如图1,在△ADC中,DP、CP分别平分∠ADC和∠ACD,
试探究∠P与∠A的数量关系,并说明理由.
(2)探究二:四边形的两个个内角与另两个内角的平分线所夹的角之间的关系
已知:如图2,在四边形ABCD中,DP、CP分别平分∠ADC和∠BCD,
试探究∠P与∠A+∠B的数量关系,并说明理由.
(3)探究三:六边形的四个内角与另两个内角的平分线所夹的角之间的关系
已知:如图3,在六边形ABCDEF中,DP、CP分别平分∠EDC和∠BCD,
请直接写出∠P与∠A+∠B+∠E+∠F的数量关系: .
相关试题

