Question

【题目】如图，BD是∠ABC的角平分线，DE∥BC，交AB于点E，∠A=45°， ∠BDC=60°。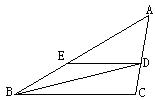

（1）求∠C的度数；
（2）求∠BED的度数.

Answer 1

【答案】
（1）

解：∵∠A=45°，∠BDC=60°，

∴∠ABD=∠BDC-∠A=15°．

∵BD是△ABC的角平分线，

∴∠DBC=∠ABD=15°，

∴∠ABC=30°，

∠C=180°-∠A-∠ABC=105°

（2）

∵DE∥BC，

∴∠AED=∠ABC=30°，

∠BED=180°-30°=150°

【解析】先根据三角形外角的性质求∠ABD，再根据角平分线的定义，可得∠DBC=∠ABD，利用三角形的内角和为180°求出∠C的度数；运用平行线的性质得∠BDE的度数，进而得出结论．
【考点精析】解答此题的关键在于理解平行线的性质的相关知识，掌握两直线平行，同位角相等；两直线平行，内错角相等；两直线平行，同旁内角互补．