【题目】如图,在ABCD中,∠BAD的平分线交BC于点E,∠BCD的平分线交AD于点F. 
(1)求证:四边形AECF是平行四边形;
(2)若AE=5,BC﹣AB=3,求四边形AECF的周长.
参考答案:
【答案】
(1)证明:如图,连接AC.
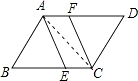
∵四边形ABCD是平行四边形,
∴AD∥BC,AD=BC,AB=CD,
∵AC平分∠BAC,FC平分∠BCD,
∴∠DAE=∠BAE,∠DCF=∠BCF.
∵AD∥BC,
∴∠DAE=∠AEB,∠DFC=∠BCF.
∴∠BAE=∠AEB,∠DFC=∠DCF,
∴AB=BE,DF=CD,
∴BE=DF.
∴AF=EC,又AD∥BC,即AF∥EC,
∴四边形AFCE是平行四边形
(2)由(1)知,AB=BE,DF=CD.
∵BC﹣AB=3,
∴BC﹣BE=EC=3.
又∵AE=5,
∴四边形AECF的周长=2(AE+EC)=2×(5+3)=16.
【解析】(1)根据角平分线的定义以及平行线的性质,证明∠BAE=∠AEB,证明AB=BE,然后证明CD=DF,即可证得AF=CE,证明四边形AECF是平行四边形;(2)利用四边形的周长公式进行解答即可.
【考点精析】本题主要考查了平行四边形的判定与性质的相关知识点,需要掌握若一直线过平行四边形两对角线的交点,则这条直线被一组对边截下的线段以对角线的交点为中点,并且这两条直线二等分此平行四边形的面积才能正确解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知不论x为何值,x2-kx-15=(x+5)(x-3),则k值为( )
A. 2 B. -2 C. 5 D. -3
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列关系一定成立的是( )
A. 若|a|=|b|,则a=b B. 若|a|=b,则a=b
C. 若|a|=﹣b,则a=b D. 若a=﹣b,则|a|=|b|
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平行四边形ABCD中,∠DAB=60°,AB=2AD,点 E、F分别是AB、CD的中点,过点A作AG∥BD,交CB的延长线于点G.

(1)求证:四边形DEBF是菱形;
(2)请判断四边形AGBD是什么特殊四边形?并加以证明. -
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,将点A(﹣2,3)向右平移a个单位长度,再向下平移b个单位长度,平移后对应的点为A′,且点A和A′关于原点对称,则a+b=_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】探究与发现:
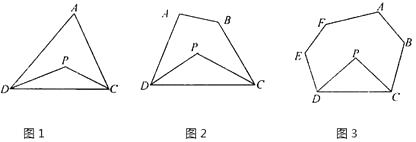
(1)探究一:三角形的一个内角与另两个内角的平分线所夹的角之间的关系
已知:如图1,在△ADC中,DP、CP分别平分∠ADC和∠ACD,
试探究∠P与∠A的数量关系,并说明理由.
(2)探究二:四边形的两个个内角与另两个内角的平分线所夹的角之间的关系
已知:如图2,在四边形ABCD中,DP、CP分别平分∠ADC和∠BCD,
试探究∠P与∠A+∠B的数量关系,并说明理由.
(3)探究三:六边形的四个内角与另两个内角的平分线所夹的角之间的关系
已知:如图3,在六边形ABCDEF中,DP、CP分别平分∠EDC和∠BCD,
请直接写出∠P与∠A+∠B+∠E+∠F的数量关系: . -
科目: 来源: 题型:
查看答案和解析>>【题目】测试五位学生的“一分钟跳绳”成绩,得到五个各不相同的数据,在统计时,出现了一处错误:将最高成绩写得更高了,计算结果不受影响的是( )
A. 方差B. 标准差C. 中位数D. 平均数
相关试题

