【题目】已知直线 y=kx+b(k≠0)过点 F(0,1),与抛物线 ![]() 相交于B、C 两点
相交于B、C 两点
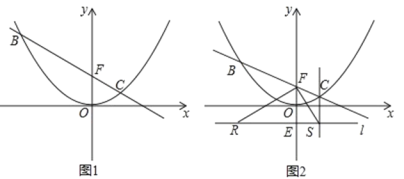
(1)如图 1,当点 C 的横坐标为 1 时,求直线 BC 的解析式;
(2)在(1)的条件下,点 M 是直线 BC 上一动点,过点 M 作 y 轴的平行线,与抛物线交于点 D, 是否存在这样的点 M,使得以 M、D、O、F 为顶点的四边形为平行四边形?若存在,求出点 M 的坐标;若不存在,请说明理由;
(3)如图 2,设 B(m,n)(m<0),过点 E(0,-1)的直线 l∥x 轴,BR⊥l 于 R,CS⊥l 于 S,连接 FR、FS.试判断△ RFS 的形状,并说明理由.
参考答案:
【答案】(1)![]() ;(2)存在;M点坐标为:(-3,
;(2)存在;M点坐标为:(-3,![]() ),
),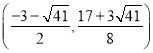 ,
,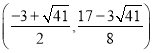 ;(3)△RFS是直角三角形;证明见详解.
;(3)△RFS是直角三角形;证明见详解.
【解析】
(1)首先求出C的坐标,然后由C、F两点用待定系数法求解析式即可;
(2)因为DM∥OF,要使以M、D、O、F为顶点的四边形为平行四边形,则DM=OF,设M(x,![]() ),则D(x,
),则D(x,![]() x2),表示出DM,分类讨论列方程求解;
x2),表示出DM,分类讨论列方程求解;
(3)根据勾股定理求出BR=BF,再由BR∥EF得到∠RFE=∠BFR,同理可得∠EFS=∠CFS,所以∠RFS=![]() ∠BFC=90°,所以△RFS是直角三角形.
∠BFC=90°,所以△RFS是直角三角形.
解:(1)因为点C在抛物线上,所以C(1,![]() ),
),
又∵直线BC过C、F两点,
故得方程组: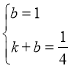
解之,得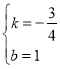 ,
,
所以直线BC的解析式为:![]() ;
;
(2)存在;理由如下:
要使以M、D、O、F为顶点的四边形为平行四边形,则MD=OF,如图1所示,
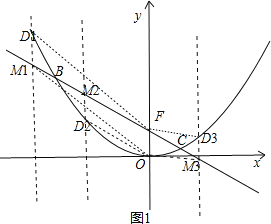
设M(x,![]() ),则D(x,
),则D(x,![]() x2),
x2),
∵MD∥y轴,
∴![]() ,
,
由MD=OF,可得:![]() ;
;
①当![]() 时,
时,
解得:x1=0(舍)或x1=-3,
所以M(-3,![]() );
);
②当![]() 时,
时,
解得:![]() ,
,
所以M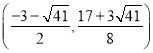 或M
或M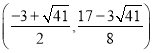 ,
,
综上所述,存在这样的点M,使以M、D、O、F为顶点的四边形为平行四边形,
M点坐标为:(-3,![]() ),
),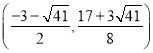 ,
,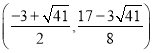 ;
;
(3)△RFS是直角三角形;理由如下:
过点F作FT⊥BR于点T,如图2所示,
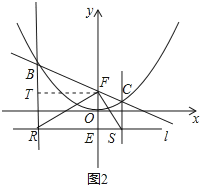
∵点B(m,n)在抛物线上,
∴m2=4n,
在Rt△BTF中,
![]()
![]()
![]()
![]() ,
,
∵n>0,
∴BF=n+1,
又∵BR=n+1,
∴BF=BR.
∴∠BRF=∠BFR,
又∵BR⊥l,EF⊥l,
∴BR∥EF,
∴∠BRF=∠RFE,
∴∠RFE=∠BFR,
同理可得∠EFS=∠CFS,
∴∠RFS=![]() ∠BFC=90°,
∠BFC=90°,
∴△RFS是直角三角形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线ykx3经过点B(-
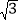 ,2),且与 x 轴交于点A.将抛物线
,2),且与 x 轴交于点A.将抛物线 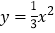 沿 x 轴作左右平移,记平移后的抛物线为C,其顶点为P.
沿 x 轴作左右平移,记平移后的抛物线为C,其顶点为P.(1)求∠OAB 的度数;
(2)抛物线
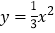 与直线 ykx3相交于 M,N两点,求△MON的面积.
与直线 ykx3相交于 M,N两点,求△MON的面积.(3)在抛物线
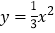 平移过程中,将△PAB 沿直线 AB 翻折得到△DAB,点D 能否落在抛物线C 上?如能,求出此时抛物线C 顶点P 的坐标;如不能,说明理由.
平移过程中,将△PAB 沿直线 AB 翻折得到△DAB,点D 能否落在抛物线C 上?如能,求出此时抛物线C 顶点P 的坐标;如不能,说明理由.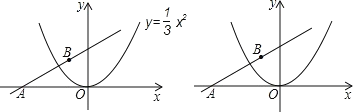
-
科目: 来源: 题型:
查看答案和解析>>【题目】A、B两辆汽车同时从相距330千米的甲、乙两地相向而行,s(千米)表示汽车与甲地的距离,t(分)表示汽车行驶的时间,如图,L1,L2分别表示两辆汽车的s与t的关系.
(1)L1表示哪辆汽车到甲地的距离与行驶时间的关系?
(2)汽车B的速度是多少?
(3)求L1,L2分别表示的两辆汽车的s与t的关系式.
(4)2小时后,两车相距多少千米?
(5)行驶多长时间后,A、B两车相遇?

-
科目: 来源: 题型:
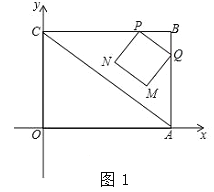
查看答案和解析>>【题目】已知矩形OABC在如图所示平面直角坐标系中,点B的坐标为(4,3),连接AC.动点P从点B出发,以2cm/s的速度,沿直线BC方向运动,运动到C为止(不包括端点B、C),过点P作PQ∥AC交线段BA于点Q,以PQ为边向下作正方形PQMN,设正方形PQMN与△ABC重叠部分图形面积为S(cm2),设点P的运动时间为t(s).
(1)请用含t的代数式表示BQ长和N点的坐标;
(2)求S与t之间的函数关系式,并指出t的取值范围;
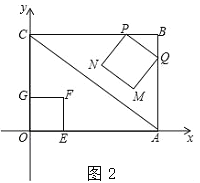
(3)如图2,点G在边OC上,且OG=1cm,在点P从点B出发的同时,另有一动点E从点O出发,以2cm/s的速度,沿x轴正方向运动,以OG、OE为一组邻边作矩形OEFG.试求当点F落在正方形PQMN的内部(不含边界)时t的取值范围.
-
科目: 来源: 题型:
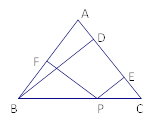
查看答案和解析>>【题目】如图,在△ABC中,AB=AC,P为BC边上任意一点,PF⊥AB于F,PE⊥AC于E,若AC边上的高BD=a.
(1)试说明PE+PF=a;
(2)若点P在BC的延长线上,其它条件不变,上述结论还成立吗?如果成立请说明理由;如果不成立,请重新给出一个关于PE,PF,a的关系式,不需要说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示双曲线y=
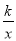 与
与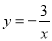 分别位于第三象限和第二象限,A是y轴上任意一点,B是
分别位于第三象限和第二象限,A是y轴上任意一点,B是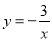 上的点,C是y=
上的点,C是y=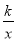 上的点,线段BC⊥x轴于D,且4BD=3CD,则下列说法:①双曲线y=
上的点,线段BC⊥x轴于D,且4BD=3CD,则下列说法:①双曲线y=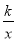 在每个象限内,y随x的增大而减小;②若点B的横坐标为-3,则C点的坐标为(-3,
在每个象限内,y随x的增大而减小;②若点B的横坐标为-3,则C点的坐标为(-3, 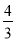 );③k=4;④△ABC的面积为定值7.正确的有( )
);③k=4;④△ABC的面积为定值7.正确的有( )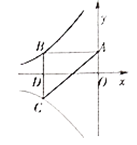
A. I个 B. 2个 C. 3个 D. 4个
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,数轴上
 两点开始时所对应的数分别是
两点开始时所对应的数分别是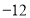 和6.
和6.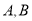 两点各自以一定的速度在数轴上运动,且
两点各自以一定的速度在数轴上运动,且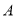 点的运动速度为2个单位长度∕秒.
点的运动速度为2个单位长度∕秒.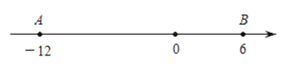
(1)若点
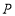 为
为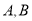 两点初始时线段
两点初始时线段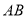 的中点,则点
的中点,则点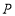 所表示的数是_____;
所表示的数是_____;(2)
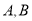 两点同时出发相向而行,在原点处相遇,求
两点同时出发相向而行,在原点处相遇,求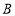 点的运动速度;
点的运动速度;(3)若
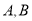 两点按(2)中的速度同时出发,向数轴正方向运动,几秒时两点相距6个单位长度?
两点按(2)中的速度同时出发,向数轴正方向运动,几秒时两点相距6个单位长度?
相关试题

