【题目】如图,在矩形![]() 中,
中,![]() ,点
,点![]() 是
是![]() 的中点,点
的中点,点![]() 为对角线
为对角线![]() 上的动点,设
上的动点,设![]() ,作
,作![]() 于点
于点![]() ,连结
,连结![]() 并延长至点
并延长至点![]() ,使得
,使得![]() ,作点
,作点![]() 关于
关于![]() 的对称点
的对称点![]() ,
,![]() 交
交![]() 于点
于点![]() ,连结
,连结![]() .
.
(1)求证:![]() ;
;
(2)当点![]() 运动到对角线
运动到对角线![]() 的中点时,求
的中点时,求![]() 的周长;
的周长;
(3)在点![]() 的运动的过程中,
的运动的过程中,![]() 是否可以为等腰三角形?若可以,求出
是否可以为等腰三角形?若可以,求出![]() 的值;若不可以,说明理由.
的值;若不可以,说明理由.
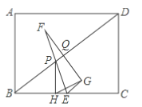
参考答案:
【答案】(1)见解析;(2)![]() ;(3)可以,
;(3)可以,![]() 的值为2或
的值为2或![]() 或
或![]()
【解析】
(1)根据三角形中位线定理即可判定;
(2)证明△BCD∽△FGE,根据相似三角形对应边长的比等于对应周长的比,可得△EFG的周长;
(3)分EH=EG,EG=GH,EH=EG三种情况讨论,根据![]() ,列方程求解即可.
,列方程求解即可.
(1)证明:∵点![]() 与点
与点![]() 关于
关于![]() 对称,
对称,
∴![]() ,
,
∵![]() ,
,
∴![]() 是
是![]() 的中位线,
的中位线,
∴![]() ;
;
(2)解:∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
当![]() 为
为![]() 的中点时,即
的中点时,即![]() ,
,
∴![]() ,此时点
,此时点![]() 与点
与点![]() 重合,如图2,
重合,如图2,
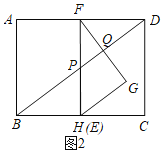
∴![]() ,
,
∴![]() ,
,
在![]() 中,
中,![]() ,
,
∴![]() ,
,
∴![]() 的周长
的周长![]() ,
,
∵![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
即![]() ,
,
∴![]() 的周长为
的周长为![]() ;
;
(3)解:在![]() 中,
中,![]() ,
,![]() ,
,
∴![]() ,则
,则![]() ,
,
∵![]() 是
是![]() 的中点,
的中点,
∴![]() ,
,
在点![]() 的运动过程中,
的运动过程中,![]() 可以为等腰三角形,有以下三种情况:
可以为等腰三角形,有以下三种情况:
①当![]() 时,如图3,
时,如图3,
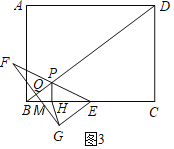
在![]() 中,
中,![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
由(1)知:![]() ,
,
∴![]() ,
,
在![]() 中,
中,![]() ,
,
即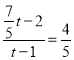 ,
,
解得![]() ;
;
②当![]() 时,如图4,过点
时,如图4,过点![]() 作
作![]() 于点
于点![]() ,
,

∴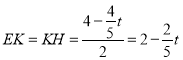 ,
,![]() ,
,
∴![]() ,
,![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
在![]() 中,
中,![]() ,
,
即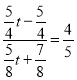 ,
,
解得![]() ;
;
③当![]() 时,如图5,延长
时,如图5,延长![]() 交
交![]() 于
于![]() ,
,
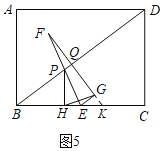
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
在![]() 中,
中,![]() ,
,
∴![]() ,
,
∴![]() ,
,
在![]() 中,
中,![]() ,
,
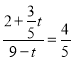 ,
,
∴![]() ,
,
综上,![]() 的值为2或
的值为2或![]() 或
或![]() 时,
时,![]() 为等腰三角形.
为等腰三角形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△ABC中,点O在斜边AB上,以O为圆心,OB为半径作圆,分别与BC,AB相交于点D,E,连结AD.已知∠CAD=∠B,
(1)求证:AD是⊙O的切线.
(2)若BC=8,tanB=
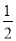 ,求⊙O 的半径.
,求⊙O 的半径.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,菱形
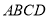 的顶点
的顶点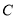 与原点
与原点 重合,点
重合,点 在
在 轴的正半轴上,点
轴的正半轴上,点 在反比例函数
在反比例函数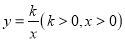 的图象上,点
的图象上,点 的坐标为
的坐标为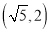 .
.(1)求
 的值;
的值;(2)若将菱形
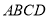 沿
沿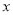 轴正方向平移,当菱形的另一个顶点恰好落在函数
轴正方向平移,当菱形的另一个顶点恰好落在函数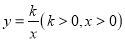 的图象上时,求菱形
的图象上时,求菱形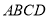 平移的距离.
平移的距离.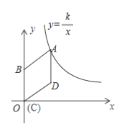
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,抛物线
 与
与 轴交于
轴交于 ,
, 两点(点
两点(点 在
在 轴的正半轴上),与
轴的正半轴上),与 轴交于点
轴交于点 ,矩形
,矩形 的一条边
的一条边 在线段
在线段 上,顶点
上,顶点 ,
,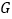 分别在线段
分别在线段 ,
, 上.
上.
 求点
求点 ,
, ,
, 的坐标;
的坐标; 若点
若点 的坐标为
的坐标为 ,矩形
,矩形 的面积为
的面积为 ,求
,求 关于
关于 的函数表达式,并指出
的函数表达式,并指出 的取值范围;
的取值范围; 当矩形
当矩形 的面积
的面积 取最大值时,
取最大值时,①求直线
 的解析式;
的解析式;②在射线
 上取一点
上取一点 ,使
,使 ,若点
,若点 恰好落在该抛物线上,则
恰好落在该抛物线上,则 ________.
________. -
科目: 来源: 题型:
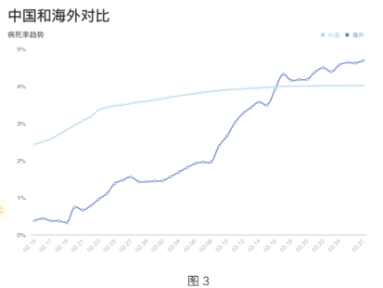
查看答案和解析>>【题目】图1是2020年3月26日全国新冠疫情数据表,图2是3月28日海外各国疫情统计表,图3是中国和海外的病死率趋势对比图,根据这些图表,选出下列说法中错误的一项( )


A.图1显示每天现有确诊数的增加量=累计确诊增加量-治愈人数增加量-死亡人数增加量.
B.图2显示美国累计确诊人数虽然约是德国的两倍,但每百万人口的确诊人数大约只有德国的一半.
C.图2显示意大利当前的治愈率高于西班牙.
D.图3显示大约从3月16日开始海外的病死率开始高于中国的病死率
-
科目: 来源: 题型:
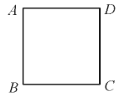
查看答案和解析>>【题目】数学课上,王老师让同学们对给定的正方形
 ,建立合适的平面直角坐标系,并表示出各顶点的坐标.下面是4名同学表示各顶点坐标的结果:
,建立合适的平面直角坐标系,并表示出各顶点的坐标.下面是4名同学表示各顶点坐标的结果:甲同学:
 ,
,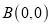 ,
,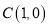 ,
,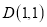 ;
;乙同学:
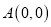 ,
,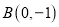 ,
,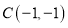 ,
,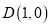 ;
;丙同学:
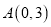 ,
,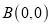 ,
,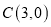 ,
,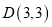 ;
;丁同学:
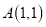 ,
,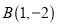 ,
,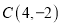 ,
,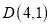 ;
;上述四名同学表示的结果中,四个点的坐标都表示正确的同学是__________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某超市随机选取1000位顾客,记录了他们购买甲、乙、丙、丁四种商品的情况,整理成如下统计表,其中“√”表示购买,“×”表示未购买.假定每位顾客购买商品的可能性相同.
商品
顾客人数
甲
乙
丙
丁
100
√
×
√
√
217
×
√
×
√
200
√
√
√
×
300
√
×
√
×
85
√
×
×
×
98
×
√
×
×
(1)估计顾客同时购买乙和丙的概率为__________.
(2)如果顾客购买了甲,并且同时也在乙、丙、丁中进行了选购,则购买__________(填乙、丙、丁)商品的可能性最大.
相关试题

