【题目】综合题
(1)如图(1),正方形AEGH的顶点E、H在正方形ABCD的边上,直接写出HD:GC:EB的结果(不必写计算过程);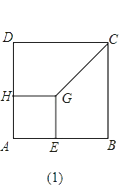
(2)将图(1)中的正方形AEGH绕点A旋转一定角度,如图(2),求HD:GC:EB;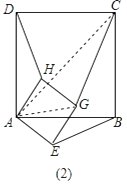
(3)把图(2)中的正方形都换成矩形,如图(3),且已知DA:AB=HA:AE=m:n,此时HD:GC:EB的值与(2)小题的结果相比有变化吗?如果有变化,直接写出变化后的结果(不必写计算过程).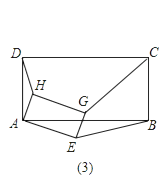
参考答案:
【答案】
(1)解:连接AG,
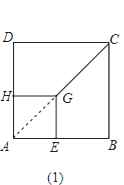
∵正方形AEGH的顶点E、H在正方形ABCD的边上,
∴∠GAE=∠CAB=45°,AE=AH,AB=AD,
∴A,G,C共线,AB﹣AE=AD﹣AH,
∴HD=BE,
∵AG= ![]() =
= ![]() AE,AC=
AE,AC= ![]() =
= ![]() AB,
AB,
∴GC=AC﹣AG= ![]() AB﹣
AB﹣ ![]() AE=
AE= ![]() (AB﹣AE)=
(AB﹣AE)= ![]() BE,
BE,
∴HD:GC:EB=1: ![]() :1;
:1;
(2)解:连接AG、AC, 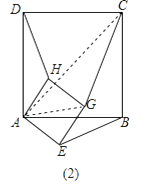
∵△ADC和△AHG都是等腰直角三角形,
∴AD:AC=AH:AG=1: ![]() ,∠DAC=∠HAG=45°,
,∠DAC=∠HAG=45°,
∴∠DAH=∠CAG,
∴△DAH∽△CAG,
∴HD:GC=AD:AC=1: ![]() ,
,
∵∠DAB=∠HAE=90°,
∴∠DAH=∠BAE,
在△DAH和△BAE中,
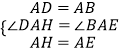 ,
,
∴△DAH≌△BAE(SAS),
∴HD=EB,
∴HD:GC:EB=1: ![]() :1;
:1;
(3)解:有变化,
连接AG、AC, 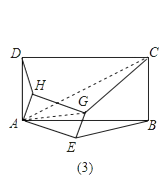
DA:AB=HA:AE=m:n,
∵∠ADC=∠AHG=90°,
∴△ADC∽△AHG,
∴AD:AC=AH:AG=m: ![]() ,∠DAC=∠HAG,
,∠DAC=∠HAG,
∴∠DAH=∠CAG,
∴△DAH∽△CAG,
∴HD:GC=AD:AC=m: ![]() ,
,
∵∠DAB=∠HAE=90°,
∴∠DAH=∠BAE,
∵DA:AB=HA:AE=m:n,
∴△ADH∽△ABE,
∴DH:BE=AD:AB=m:n,
∴HD:GC:EB=m: ![]() :n.
:n.
【解析】(1)首先连接AG,由正方形AEGH的顶点E、H在正方形ABCD的边上,易证得∠GAE=∠CAB=45°,AE=AH,AB=AD,即A,G,C共线,继而可得HD=BE,GC=![]() BE,即可求得HD:GC:EB的值;
BE,即可求得HD:GC:EB的值;
(2)连接AG、AC,由△ADC和△AHG都是等腰直角三角形,易证得△DAH∽△CAG与△DAH≌△BAE,利用相似三角形的对应边成比例与全等三角形的性质,即可求得HD:GC:EB的值;
(3)连接AG、AC, 由DA:AB=HA:AE=m:n,易证得△ADC∽△AHG,△DAH∽△CAG,△ADH∽△ABE,利用相似三角形的对应边成比例与勾股定理即可求得HD:GC:EB的值
【考点精析】关于本题考查的等腰直角三角形和勾股定理的概念,需要了解等腰直角三角形是两条直角边相等的直角三角形;等腰直角三角形的两个底角相等且等于45°;直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2才能得出正确答案.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列图形中,是轴对称图形但不是中心对称图形的是( )
A.
B.
C.
D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某商场销售一种西装和领带,西装每套定价200元,领带每条定价40元.国庆节期间商场决定开展促销活动,活动期间向客户提供两种优惠方案:
方案一:买一套西装送一条领带;
方案二:西装和领带都按定价的90%付款.
现某客户要到该商场购买西装20套,领带x
 .
.(1)若该客户按方案一购买,需付款多少元(用含x的式子表示)?若该客户按方案二购买,需付款多少元(用含x的式子表示)?
(2)若
 ,通过计算说明此时按哪种方案购买较为合算;
,通过计算说明此时按哪种方案购买较为合算;(3)当
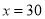 时,你能给出一种更为省钱的购买方法吗?试写出你的购买方法和所需费用.
时,你能给出一种更为省钱的购买方法吗?试写出你的购买方法和所需费用. -
科目: 来源: 题型:
查看答案和解析>>【题目】在下列图形中,既是轴对称图形,又是中心对称图形的是( )
A. 直角三角形
直角三角形
B. 正五边形
正五边形
C. 正方形
正方形
D. 平行四边形
平行四边形 -
科目: 来源: 题型:
查看答案和解析>>【题目】下列图形中,是轴对称图形,不是中心对称图形的是( )
A.
B.
C.
D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】周末,小明坐公交车到滨海公园游玩,他从家出发0.8小时后达到中心书城,逗留一段时间后继续坐公交车到滨海公园,小明离家一段时间后,爸爸驾车沿相同的路线前往海滨公园. 如图是他们离家路程s(km)与小明离家时间t(h)的关系图,请根据图回答下列问题:
(1)图中自变量是____,因变量是______;
(2)小明家到滨海公园的路程为____ km,小明在中心书城逗留的时间为____ h;
(3)小明出发______小时后爸爸驾车出发;
(4)图中A点表示___________________________________;
(5)小明从中心书城到滨海公园的平均速度为______km/h,小明爸爸驾车的平均速度为______km/h;(补充;爸爸驾车经过______追上小明);
(6)小明从家到中心书城时,他离家路程s与坐车时间t之间的关系式为________.

-
科目: 来源: 题型:
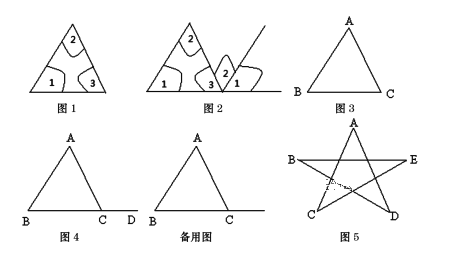
查看答案和解析>>【题目】下列是某初一数学兴趣小组探究三角形内角和的过程,请根据他们的探究过程,结合所学知识,解答下列问题.兴趣小组将图1△ABC三个内角剪拼成图2,由此得△ABC三个内角的和为180度.
(1)请利用图3证明上述结论.
(2)三角形的一条边与另一条边的反向延长线组成的角,叫做三角形的外角.
如图4,点D为BC延长线上一点,则∠ACD为△ABC的一个外角.
①请探究出∠ACD与∠A、∠B的关系,并直接填空:∠ACD=______.
②如图5是一个五角星,请利用上述结论求∠A+∠B+∠C+∠D+∠E的值.
相关试题

