【题目】阅读下列短文:
如图,G是四边形ABCD对角线AC上一点,过G作GE∥CD交AD于E,GF∥CB交AB于F,若EG=FG,则有BC=CD成立,同时可知四边形ABCD与四边形AFGE相似.

解答问题:
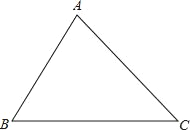
(1)有一块三角形空地(如图△ABC),BC邻近公路,现需在此空地上修建一个正方形广场,其余地为草坪,要使广场一边靠公路,且其面积最大,如何设计,请你在下面图中画出此广场正方形.(尺规作图,不写作法)
(2)锐角△ABC是一块三角形余料,边AB=130mm,BC=150mm,AC=140mm,要把它加工成正方形零件,使正方形的一边在三角形的一边上,其余两个顶点分别在另外两条边上,且剪去正方形零件后剩下的边角料较少,这个正方形零件的边长是多少?你能得出什么结论,并证明你的结论.
参考答案:
【答案】(1)见解析;(2)见解析
【解析】试题分析:(1)先在AB上任取一点O,过O作BC的垂线,然后作出以OM为一边的正方形OMNP,连接BP并延长交AC于点E,过点E作BC的垂线交BC于点H,再以EH为边作正方形EFGH即可;
(2)过A作AD⊥BC于点D,在Rt△ABD与Rt△ACD中,根据AD是公共边利用勾股定理列式求出BD的长,再利用勾股定理求出AD的长,然后利用△ABC的面积求出AB、AC边上的高,设正方形的边长为a,根据相似三角形对应高的比等于对应边的比列出比例式求解得到正方形的边长与三角形的边与相应边上的高的关系,然后判断出当边与边上的高的和最小时,正方形的边长最大,剪去正方形零件后剩下的边角料较少,然后计算即可得解.
试题解析:(1)如图;
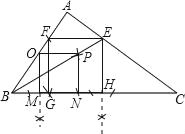
(2)如图,过A作AD⊥BC于点D,则CD=BC﹣BD=150﹣BD,
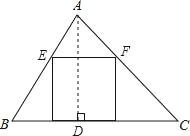
在Rt△ABD中,AD2=AB2﹣BD2=1302﹣BD2,
在Rt△ACD中,AD2=AC2﹣CD2=1402﹣(150﹣BD)2,
所以,1302﹣BD2=1402﹣(150﹣BD)2,
解得BD=![]() =66,
=66,
所以,AD2=1302﹣662=12544,
AD=112mm,
设AB、AC边上的高分别为hAB,hAC,
则S△ABC=![]() ×130×hAB=
×130×hAB=![]() ×140×hAC=
×140×hAC=![]() ×150×112,
×150×112,
解得hAB=129![]() mm,hAC=120mm,
mm,hAC=120mm,
设正方形的边长为a,
∵EF∥BC,
∴△AEF∽△ABC,
∴![]() ,
,
即![]() ,
,
整理得,a=![]() ,
,
∵BCAD是△ABC面积的2倍,
∴BC+AD,也就是三角形一条边与这条边上的高的和越小,则加工成的正方形的边长越大,面积也就是越大,剪去正方形零件后剩下的边角料较少,
130+129![]() =259
=259![]() mm,
mm,
140+120=260mm,
150+112=262mm,
∵259![]() <260<262,
<260<262,
∴有两个顶点在AB=130mm边上加工成的正方形的面积最大,
这个正方形的边长为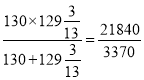 =64
=64![]() mm.
mm.
结论:正方形的一条边在三角形的哪一条边上,则正方形的边长等于这条边与这条边上的高的积除以它们的和,并且最短边上的正方形的边长最大.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知M的横坐标是
 的平方根,纵坐标是2,且点M到y轴的距离是到x轴的距离的3倍。
的平方根,纵坐标是2,且点M到y轴的距离是到x轴的距离的3倍。(1)求a的值;
(2)求点M的坐标。
-
科目: 来源: 题型:
查看答案和解析>>【题目】岳飞是我国古代宋朝的民族英雄,曾任通泰镇抚史、兼泰州知州.据说在泰州抗击金兵期间,有一次曾向将领们讲了如下一个布阵图,如图4是一座城池,在城池的四周设了八个哨所,一共由24个卫士把守,按直线算,每边都有11个人,后来由于军情发生变化,连续四次给哨所增添兵力,每次增加4人,但要求在增加人员后,仍然保持每边11个人把守.请问,兵力应如何调整?
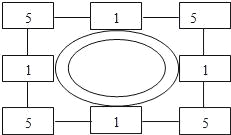
-
科目: 来源: 题型:
查看答案和解析>>【题目】某中学七年级有350名师生需要租车去野外进行拓展训练,现有A、B两种类型号的车可供选择,已知1辆A型车和2辆B型车可载110人,2辆A型车和1辆B型车可载100人。
(1)A、B型车每辆可分别载多少人?
(2)要始每辆车都恰好坐满且正好运完这些师生,请问你有哪几种设计租车方案,请一一列举出来。
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知A、B两地相距4800米,甲从A地出发步行到B地,20分钟后乙从B地出发骑自行车到A地,设甲步行的时间为x分钟,甲、乙两人离A地的距离分别为
 米、
米、 米,
米, 、
、 与x的函数关系图象如图所示,根据图象解答下列问题:
与x的函数关系图象如图所示,根据图象解答下列问题:
(1)直接写出y
 、y
、y 与x的函数关系式,并写出自变量x的取值范围;
与x的函数关系式,并写出自变量x的取值范围;(2)求甲出发后多少分钟两人相遇,相遇时乙离A地多少米?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线
 分别交x轴、y轴于A、B两点,直线BC与x轴交于点
分别交x轴、y轴于A、B两点,直线BC与x轴交于点 ,P是线段AB上的一个动点
,P是线段AB上的一个动点 点P与A、B不重合
点P与A、B不重合 .
.
(1)求直线BC所对应的的函数表达式;
(2)设动点P的横坐标为t,
 的面积为S.
的面积为S.①求出S与t的函数关系式,并写出自变量t的取值范围;
②在线段BC上存在点Q,使得四边形COPQ是平行四边形,求此时点Q的坐标.
相关试题

