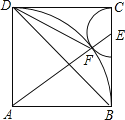
【题目】如图,在正方形ABCD中,E是BC边上的一点,以E为圆心,EC为半径的半圆与以A为圆心AB为半径的圆弧相外切于点F,若AB=4,
(1)求半圆E的半径r的长;
(2)求四边形ADCE的面积;
(3)连接DB、DF,设∠BDF=α,∠AEC=β,求证:β-2α=90°.

参考答案:
【答案】(1)1;(2)10;(3)证明见解析.
【解析】分析:
(1)根据正方形的性质求出AB、AE、BE的长,在Rt△ABE中根据勾股定理得出方程,求出方程的解即可;
(2)根据梯形的面积公式求出即可;
(3)根据三角形的外角性质求出β=∠BAE+90°,根据圆周角定理得出∠BDF=![]() ∠BAE,代入求出即可.
∠BAE,代入求出即可.
本题解析:
(1)在Rt△ABE中,AB=BC=AF=AD=DC=4,
BE=BCCE=4r,AE=BF+EF=4+r,
∵AE=AB+BE,
∴(4+r)=4+(4r),
解得:r=1,
答:半E的半径r的长是1.
(2)梯形ADCE的面积是S=![]() DC(AD+CE)=
DC(AD+CE)= ![]() ×4×(4+1)=10,
×4×(4+1)=10,
答:四边形ADCE的面积是10.
(3)证明:∵∠AEC是Rt△ABE的外角,
∴β=∠BAE+90°,
∵∠BDF=![]() ∠BAE,
∠BAE,
∴α=![]() ∠BAE,
∠BAE,
即∠BAE=2α,
∴β=2α+90°,
即β2α=90°.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠ABC的平分线BF与△ABC的外角平分线CF相交于点F,过F作DF∥BC,交AB于D,交AC于E。
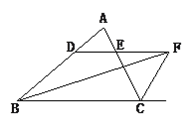
(1)写出图中所有的等腰三角形,并选择其中一个说明理由。
(2)直接写出BD,CE,DE之间的数量关系。
(3)若DE=5cm,CE=8cm,BF=24cm,求△BDF的面积。
-
科目: 来源: 题型:
查看答案和解析>>【题目】如果出售一个商品,获利记为正,则-20元表示。
-
科目: 来源: 题型:
查看答案和解析>>【题目】一个角的补角是它的余角的4倍,则这个角是_________度.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某校规定:学生的数学学期综合成绩是由平时、期中和期末三项成绩按3:3:4的比例计算所得.若某同学本学期数学的平时、期中和期末成绩分别是90分,90分和85分,则他本学期数学学期综合成绩是 分.
-
科目: 来源: 题型:
查看答案和解析>>【题目】用代数式表示“a的3倍与1的差”:。
-
科目: 来源: 题型:
查看答案和解析>>【题目】在下列条件中,△ABC不是直角三角形的是( )
A. b2=a2-c2 B. a2:b2:c2=1:3:2
C. ∠A:∠B:∠C=3:4:5 D. ∠A+∠B=∠C
相关试题

