【题目】用一根长度为![]() 的细绳围成一个等腰三角形.
的细绳围成一个等腰三角形.
(1)如果所围等腰三角形的腰长是底边长的2倍,则此时的底边长度是多少?
(2)所围成的等腰三角形的腰长不可能等于![]() ,请简单说明原因.
,请简单说明原因.
(3)若所围成的等腰三角形的腰长为![]() ,请求出
,请求出![]() 的取值范围.
的取值范围.
参考答案:
【答案】(1)此时的底边长度是![]() ;(2)所围成的等腰三角形的腰长不可能等于
;(2)所围成的等腰三角形的腰长不可能等于![]() ;(3)
;(3)![]() .
.
【解析】
(1)设底边长为xcm,则腰长为2xcm,根据周长公式列一元一次方程,解方程即可求得底边的长;
(2)由题意直接利用三角形三边关系进行检验即可说明原因;
(3)假设所围成的等腰三角形的腰长为![]() ,由题意直接利用三角形三边关系列不等式组进而即可求出
,由题意直接利用三角形三边关系列不等式组进而即可求出![]() 的取值范围.
的取值范围.
解:(1)设底边长度为![]() ,
,
∵腰长是底边的2倍,
∴腰长为![]() ,
,
∴![]() ,
,
解得,![]() ,
,
∴此时的底边长度是![]() .
.
(2)原因:假设可以围成腰长为4的等腰三角形,则该三角形的三边长分别为:![]() ,
,![]() ,
,![]() ,
,
∵![]() ,
,
∴无法构成三角形,故所围成的等腰三角形的腰长不可能等于![]() .
.
(3)∵等腰三角形的腰长为![]() ,
,
∴等腰三角形的底边长为![]() ,由
,由![]() ,得
,得![]() ,
,
∴![]() 的取值范围为:
的取值范围为:![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形
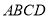 中,
中,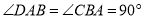 ,将
,将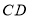 绕点
绕点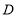 逆时针旋转
逆时针旋转 至
至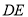 ,连接
,连接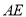 ,若
,若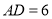 ,
,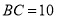 ,则
,则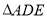 的面积是( )
的面积是( )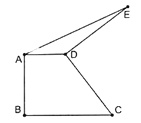
A.
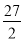 B.12C.9D.8
B.12C.9D.8 -
科目: 来源: 题型:
查看答案和解析>>【题目】在直角三角形
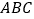 中,
中,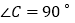 ,
, ,以
,以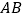 为边作正方形
为边作正方形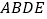 ,连接
,连接 、
、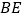 交
交 ,
,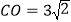 ,则
,则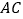 的长为( )
的长为( )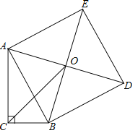
A.
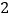 B.
B.  C.
C. 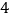 D.
D. 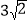
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知在
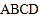 中,
中,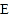 ,
,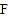 分别是
分别是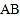 ,
,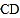 的中点,
的中点,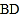 是对角线,
是对角线,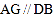 交
交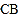 延长线于
延长线于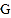 .若四边形
.若四边形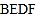 是菱形,则四边形
是菱形,则四边形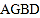 是( )
是( )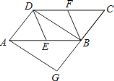
A. 平行四边形 B. 矩形
C. 菱形 D. 正方形
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,把矩形纸片ABCD沿EF翻折,点A恰好落在BC边的A′处,若AB=
 ,∠EFA=60°,则四边形A′B′EF的周长是( )
,∠EFA=60°,则四边形A′B′EF的周长是( )
A. 1+3
 B. 3+
B. 3+ C. 4+
C. 4+ D. 5+
D. 5+
-
科目: 来源: 题型:
查看答案和解析>>【题目】我国的动车和高铁技术处于全球领先位置,是“中国制造”的闪亮名片,高铁和普通列车的双普及模式,极大方便了人民群众出行.上世纪60年代通车的京广铁路广州一长沙段全程1000公里,而广州至长沙的高铁里程是普通列车铁路里程的
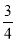 .
.(1)广州至长沙的高铁里程是______公里;
(2)若广州至长沙的高铁平均速度(公里/小时)是普通列车平均速度(公里/小时)的2.5倍,且乘坐高铁所需时间比乘坐普通列车所需时间少7个小时,求高铁的平均速度.
-
科目: 来源: 题型:
查看答案和解析>>【题目】勾股定理是人类最伟大的科学发现之一,在我国古算书《周髀算经》中早有记载.如图1,以直角三角形的各边为边分别向外作正方形,再把较小的两张正方形纸片按图2的方式放置在最大正方形内.若知道图中阴影部分的面积,则一定能求出( )

A.直角三角形的面积
B.最大正方形的面积
C.较小两个正方形重叠部分的面积
D.最大正方形与直角三角形的面积和
相关试题

