【题目】已知⊙O的半径为3,△ABC内接于⊙O,AB=3 ![]() ,AC=3
,AC=3 ![]() ,D是⊙O上一点,且AD=3,则CD的长应是( )
,D是⊙O上一点,且AD=3,则CD的长应是( )
A.3
B.6
C.![]()
D.3或6
参考答案:
【答案】D
【解析】解:第一种情况,当点D在AC弧上时,连接OA、OC、OD.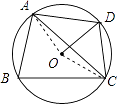
所以AD=OA=OC=OD=3,△AOD是等边三角形,∠ADO=∠DAO=∠AOD=60°.
过O作OP垂直弦AC于P,根据垂径定理,PA=PC= ![]() AC=
AC= ![]() .
.
∴在Rt△AOP中,OP= ![]() ,
,
∴∠OAP=30°,∠AOP=60°=∠AOD.
∴OP与OD重合,即OD垂直平分弦AC,所以CD=AD=3.
第二种情况:当点D在AB弧上时,同理得△AOD是等边三角形,∠AOD=60°.
由(1)知∠AOC=120°.
∴∠AOD+∠AOC=180°,即D、O、C在同一直线上,故CD=6.
故选D.
【考点精析】利用勾股定理的概念和垂径定理对题目进行判断即可得到答案,需要熟知直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2;垂径定理:平分弦(不是直径)的直径垂直于弦,并且平分弦所对的两条弧.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知关于x,
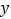 的方程组
的方程组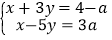 ,给出下列结论:①
,给出下列结论:①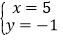 是方程组的解;②无论a取何值, x,y的值都不可能互为相反数;③当a=1时,方程组的解也是方程x+y=4﹣a的解;④
是方程组的解;②无论a取何值, x,y的值都不可能互为相反数;③当a=1时,方程组的解也是方程x+y=4﹣a的解;④ ,
, 都为自然数的解有4对.其中正确的为______________.
都为自然数的解有4对.其中正确的为______________. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC的三边AB、BC、CA的长分别为40、50、60,其三条角平分线交于点O,则S△ABO:S△BCO:S△CAO等于 ( )
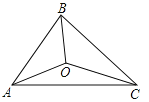
A. 1:2:3 B. 2:3:4 C. 3:4:5 D. 4:5:6
-
科目: 来源: 题型:
查看答案和解析>>【题目】(9分) “先学后教”课题组对学生参与小组合作的深度和广度进行评价,其评价项目为主动质疑、独立思考、专注听讲、讲解题目四项.课题组随机抽取了若干名初中学生的参与情况,绘制了如图两幅不完整的统计图,请根据图中所给信息解答下列问题:

(1)在这次评价中,一共抽查了______名学生;
(2)请将条形统计图补充完整;
(3)求出扇形统计图中,“主动质疑”所对应扇形的圆心角的度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】圆的半径扩大到原来的3倍,周长扩大到原来的____倍.面积扩大到原来的_______倍.
-
科目: 来源: 题型:
查看答案和解析>>【题目】二次函数y=ax2+bx+c(a>0)的顶点为P,其图像与x轴有两个交点A(﹣m,0),B(1,0),交y轴于点C(0,﹣3am+6a),以下说法:
①m=3;
②当∠APB=120°时,a= ;
;
③当∠APB=120°时,抛物线上存在点M(M与P不重合),使得△ABM是顶角为120°的等腰三角形;
④抛物线上存在点N,当△ABN为直角三角形时,有a≥
正确的是( )
A.①②
B.③④
C.①②③
D.①②③④ -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,抛物线y=ax2+bx+c(a>0)的对称轴是过点(1,0)且平行于y轴的直线,若点P(4,0)在该抛物线上,则4a﹣2b+c的值为

相关试题

