【题目】如图(1),AB=4cm,AC⊥AB于A,BD⊥AB于B,AC=BD=3cm.点P在线段AB上以lcm/s的速度由点A向点B运动,同时,点Q在线段BD上由点B向点D运动.它们运动的时间为t(s).

(1)若点Q的运动速度与点P的运动速度相等,当t=l时,△ACP与△BPQ是否全等?PC与PQ是否垂直?请分别说明理由;
(2)如图(2),将图(1)中的“AC上AB于A,BD上AB于B”改为“∠CAB=∠DBA=60![]() ”,其他条件不变.设点Q的运动速度为x cm/s,是否存在实数x,使得△ACP与△BPQ全等?若存在,求出相应的x、t的值;若不存在,请说明理由.
”,其他条件不变.设点Q的运动速度为x cm/s,是否存在实数x,使得△ACP与△BPQ全等?若存在,求出相应的x、t的值;若不存在,请说明理由.
参考答案:
【答案】(1) △ACP≌△BPQ,PC垂直于PQ,理由见解析.(2)存在,见解析.
【解析】试题分析:(1)利用SAS证得△ACP≌△BPQ,得出∠ACP=∠BPQ,进一步得出∠APC+∠BPQ=∠APC+∠ACP=90°得出结论即可;
(2)由△ACP≌△BPQ,分两种情况:①AC=BP,AP=BQ,②AC=BQ,AP=BP,建立方程组求得答案即可.
试题解析:(1)当t=1时,△ACP≌△BPQ,PC垂直于PQ
理由如下:
当t=1时,AP=BQ=1,BP=AC=3,
又∠A=∠B=90°,
∴在△ACP和△BPQ中,
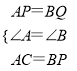
∴△ACP≌△BPQ.
∴∠ACP=∠BPQ,
∴∠APC+∠BPQ=∠APC+∠ACP=90°.
∴∠CPQ=90°,即线段PC与线段PQ垂直.
(2)①若△ACP≌△BPQ,
则AC=BP,AP=BQ,
![]()
解得![]()
②若△ACP≌△BQP,
则AC=BQ,AP=BP,
![]() 解得
解得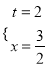
综上所述,存在![]() 或
或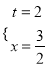 使得△ACP与△BPQ全等.
使得△ACP与△BPQ全等.
-
科目: 来源: 题型:
查看答案和解析>>【题目】定义:对于给定的两个函数,任取自变量x的一个值,当x<0时,它们对应的函数值互为相反数;当x≥0时,它们对应的函数值相等,我们称这样的两个函数互为相关函数.例如:一次函数y=x﹣1,它的相关函数为
 .
.(1)已知点A(﹣5,8)在一次函数y=ax﹣3的相关函数的图象上,求a的值;
(2)已知二次函数
 .
.①当点B(m,
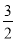 )在这个函数的相关函数的图象上时,求m的值;
)在这个函数的相关函数的图象上时,求m的值;②当﹣3≤x≤3时,求函数
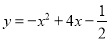 的相关函数的最大值和最小值;
的相关函数的最大值和最小值;(3)在平面直角坐标系中,点M,N的坐标分别为(﹣
 ,1),(
,1),( ,1}),连结MN.直接写出线段MN与二次函数
,1}),连结MN.直接写出线段MN与二次函数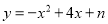 的相关函数的图象有两个公共点时n的取值范围.
的相关函数的图象有两个公共点时n的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系内,已知A(2x,3x+1).
(1)点A在x轴下方,在y轴的左侧,且到两坐标轴的距离相等,求x的值;
(2)若x=1,点B在x轴上,且S△OAB=6,求点B的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,已知点A(0,4),B(8,0),C(8,6)三点.

(1)求△ABC的面积;
(2)如果在第二象限内有一点P(m,1),且四边形ABOP的面积是△ABC的面积的两倍;求满足条件的P点的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列命题是真命题的是( )
A.内错角相等
B.平面内,过一点有且只有一条直线与已知直线垂直
C.相等的角是对顶角
D.过一点有且只有一条直线与已知直线平行
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点P是等边△ABC内一点,PA=6,PB=8,PC=10,则△APC的面积是__________

-
科目: 来源: 题型:
查看答案和解析>>【题目】射阳县实验初中为了解全校学生上学期参加社区活动的情况,学校随机调查了本校50名学生参加社区活动的次数,并将调查所得的数据整理如下:
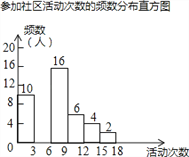
参加社区活动次数的频数、频率分布表
活动次数x
频数
频率
0<x≤3
10
0.20
3<x≤6
a
0.24
6<x≤9
16
0.32
9<x≤12
6
0.12
12<x≤15
m
b
15<x≤18
2
n
根据以上图表信息,解答下列问题:
(1)表中a= ,b= ;
(2)请把频数分布直方图补充完整(画图后请标注相应的数据);
(3)若该校共有1200名学生,请估计该校在上学期参加社区活动超过6次的学生有多少人?
相关试题

