【题目】某商场销售的篮球和足球的进货价格分别是每个30元,40元.商场销售5个篮球和1个足球,可获利76元;销售6个篮球和3个足球,可获利120元.
(1)求该商场篮球和足球的销售价格分别是多少?
(2)商场准备用不多于2500元的资金购进篮球和足球共70个,问最少需要购进篮球多少个?
参考答案:
【答案】(1)篮球的售价为42元,足球的售价为56元;(2)30个
【解析】
(1)设该商场篮球的售价为x元,足球的售价为y元,根据“商场销售5个篮球和1个足球,可获利76元;销售6个篮球和3个足球,可获利120元”,即可得出关于x,y的二元一次方程组,解之即可得出结论;
(2)设购进篮球m个,则购进足球(70﹣m)个,根据总价=单价×数量结合总价不多于2500元,即可得出关于m的一元一次不等式,解之取其最小值即可得出结论.
解:(1)设该商场篮球的售价为x元,足球的售价为y元,
依题意,得: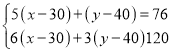 ,
,
解得:![]() .
.
答:该商场篮球的售价为42元,足球的售价为56元.
(2)设购进篮球m个,则购进足球(70﹣m)个,
依题意,得:30m+40(70﹣m)≤2500,
解得:m≥30.
答:最少需要购进篮球30个.
故答案是:(1)篮球的售价为42元,足球的售价为56元;(2)30个
-
科目: 来源: 题型:
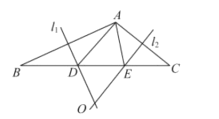
查看答案和解析>>【题目】如图,在△ABC中,边AB的垂直平分线OM与边AC的垂直平分线ON交于点O,分别交BC于点D、E,已知△ADE的周长5cm.
(1)求BC的长;
(2)分别连接OA、OB、OC,若△OBC的周长为13cm,求OA的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,CD⊥DA,DA⊥AB,∠1=∠2.试确定射线DF与AE的位置关系,并说明你的理由.

(1)问题的结论:DF______AE.
(2)证明思路欲证DF______AE,只要证∠3=______.
(3)证明过程:
证明:∵CD⊥DA,DA⊥AB,( )
∴∠CDA=∠DAB=______°(垂直定义)
∵∠1=∠2,( )
∴∠CDA-∠1=______-______,(等式的性质)
即∠3=______
∴DF______AE( , )
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系xOy中,双曲线y=
 与直线y=﹣2x+2交于点A(﹣1,a).
与直线y=﹣2x+2交于点A(﹣1,a).(1)求a,m的值;
(2)求该双曲线与直线y=﹣2x+2另一个交点B的坐标.

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,在△ABC中,BC=AC,以BC为直径的⊙O与边AB相交于点D,DE⊥AC,垂足为点E.
(1)求证:点D是AB的中点;
(2)判断DE与⊙O的位置关系,并证明你的结论;
(3)若⊙O的直径为18,cosB=
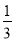 ,求DE的长.
,求DE的长.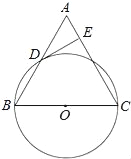
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC是等边三角形,延长BC到E,使CE=
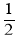 BC.点D是边AC的中点,连接ED并延长ED交AB于F,求证:
BC.点D是边AC的中点,连接ED并延长ED交AB于F,求证:(1)EF⊥AB;(2)DE=2DF.
-
科目: 来源: 题型:
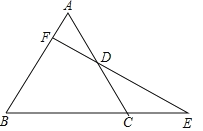
查看答案和解析>>【题目】数学课上,李老师出示了如下框中的题目.
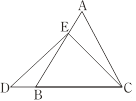
在等边三角形ABC中,点E在AB上,点D在CB的延长线上,且ED=EC,如图.试确定线段AE与DB的大小关系,并说明理由.
小敏与同桌小聪讨论后,进行了如下解答:
(1)特殊情况,探索结论
当点E为AB的中点时,如图1,确定线段AE与的DB大小关系.请你直接写出结论:
AE DB(填“>”,“<”或“=”).
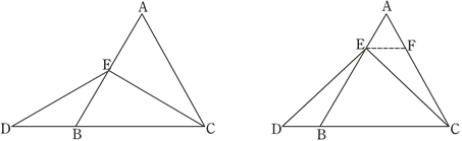
图1 图2
(2)特例启发,解答题目
解:题目中,AE与DB的大小关系是:AE DB(填“>”,“<”或“=”).
理由如下:如图2,过点E作EF∥BC,交AC于点F.
(请你完成以下解答过程)
(3)拓展结论,设计新题
在等边三角形ABC中,点E在直线AB上,点D在直线BC上,且ED=EC.若△ABC的边长为1,AE=2,求CD的长(请你直接写出结果).
相关试题

