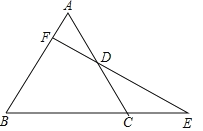
【题目】如图,△ABC是等边三角形,延长BC到E,使CE=![]() BC.点D是边AC的中点,连接ED并延长ED交AB于F,求证:
BC.点D是边AC的中点,连接ED并延长ED交AB于F,求证:
(1)EF⊥AB;(2)DE=2DF.
参考答案:
【答案】(1)见解析;(2)见解析
【解析】
(1)根据等边三角形的性质得出AC=BC,∠ACB=∠B=60°,求出CD=CE,根据三角形外角性质和等腰三角形的性质求出∠E=30°,求出∠BFE即可;
(2)连接BD,求出BD=DE,根据含30°角的直角三角形的性质得出BD=2DF,即可得出答案.
证明:(1)∵△ABC是等边三角形,
∴AC=BC,∠ACB=∠B=60°,
∵D为AC的中点,
∴AD=CD=![]() AC,
AC,
∵CE=![]() BC,
BC,
∴CD=CE,
∵∠E+∠CDE=∠ACB=60°,
∴∠E=∠CDE=30°,
∵∠B=60°,
∴∠EFB=180°﹣60°﹣30°=90°,
即EF⊥AB;
(2)连接BD,

∵△ABC是等边三角形,
∴AB=BC,∠ABC=60°,
∵D为AC的中点,
∴∠DBC=∠ABD=![]() ∠ABC=30°,
∠ABC=30°,
∵∠E=30°,
∴∠DBC=∠E,
∴DE=BD,
∵∠BFE=90°,∠ABD=30°,
∴BD=2DF,
即DE=2DF.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系xOy中,双曲线y=
 与直线y=﹣2x+2交于点A(﹣1,a).
与直线y=﹣2x+2交于点A(﹣1,a).(1)求a,m的值;
(2)求该双曲线与直线y=﹣2x+2另一个交点B的坐标.

-
科目: 来源: 题型:
查看答案和解析>>【题目】某商场销售的篮球和足球的进货价格分别是每个30元,40元.商场销售5个篮球和1个足球,可获利76元;销售6个篮球和3个足球,可获利120元.
(1)求该商场篮球和足球的销售价格分别是多少?
(2)商场准备用不多于2500元的资金购进篮球和足球共70个,问最少需要购进篮球多少个?
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,在△ABC中,BC=AC,以BC为直径的⊙O与边AB相交于点D,DE⊥AC,垂足为点E.
(1)求证:点D是AB的中点;
(2)判断DE与⊙O的位置关系,并证明你的结论;
(3)若⊙O的直径为18,cosB=
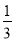 ,求DE的长.
,求DE的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】数学课上,李老师出示了如下框中的题目.
在等边三角形ABC中,点E在AB上,点D在CB的延长线上,且ED=EC,如图.试确定线段AE与DB的大小关系,并说明理由.
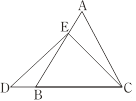
小敏与同桌小聪讨论后,进行了如下解答:
(1)特殊情况,探索结论
当点E为AB的中点时,如图1,确定线段AE与的DB大小关系.请你直接写出结论:
AE DB(填“>”,“<”或“=”).
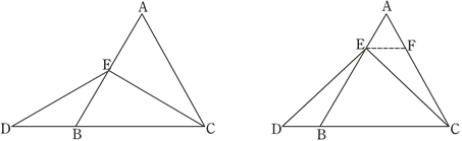
图1 图2
(2)特例启发,解答题目
解:题目中,AE与DB的大小关系是:AE DB(填“>”,“<”或“=”).
理由如下:如图2,过点E作EF∥BC,交AC于点F.
(请你完成以下解答过程)
(3)拓展结论,设计新题
在等边三角形ABC中,点E在直线AB上,点D在直线BC上,且ED=EC.若△ABC的边长为1,AE=2,求CD的长(请你直接写出结果).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠B=32°,将△ABC沿直线m翻折,点B落在点D的位置,则∠1-∠2的度数是( )
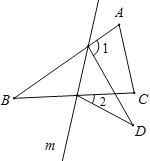
A. 32° B. 64° C. 65° D. 70°
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点A的坐标为(8,0),点B为y轴负半轴上的一动点,分别以OB,AB为直角边在第三、第四象限作等腰直角三角形OBF,等腰直角三角形ABE,连接EF交y轴与P点,当点B在y轴上移动时,则PB的长度是( )
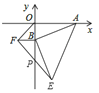
A.2B.4C.不是已知数的定值D.PB的长度随点B的运动而变化
相关试题

