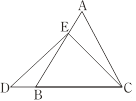
【题目】数学课上,李老师出示了如下框中的题目.
在等边三角形ABC中,点E在AB上,点D在CB的延长线上,且ED=EC,如图.试确定线段AE与DB的大小关系,并说明理由. |
|
小敏与同桌小聪讨论后,进行了如下解答:
(1)特殊情况,探索结论
当点E为AB的中点时,如图1,确定线段AE与的DB大小关系.请你直接写出结论:
AE DB(填“>”,“<”或“=”).
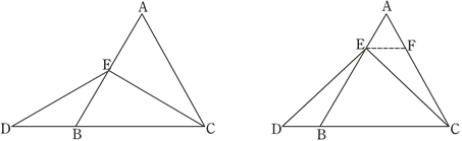
图1 图2
(2)特例启发,解答题目
解:题目中,AE与DB的大小关系是:AE DB(填“>”,“<”或“=”).
理由如下:如图2,过点E作EF∥BC,交AC于点F.
(请你完成以下解答过程)
(3)拓展结论,设计新题
在等边三角形ABC中,点E在直线AB上,点D在直线BC上,且ED=EC.若△ABC的边长为1,AE=2,求CD的长(请你直接写出结果).
参考答案:
【答案】(1)=;(2)=,过程见解析;(3)CD的长是1或3.
【解析】试题分析:(1)根据△ABC是等边三角形,点E为AB的中点,即可得出CE⊥AB,进而得出∠ECB=∠D=∠DEB=30°,即可得出线段AE与DB的大小关系;
(2)首先得出BE=CF,进而得出∠EDB=∠ECB,∠BED=∠FCE,进而利用△DBE≌△EFC即可得出答案;
(3)分两种情况进行讨论,①当E在线段BA的延长线上,D在线段BC的延长线上;②当E在线段AB的延长线上,D在线段CB的延长线上.
试题解析:(1)∵△ABC是等边三角形,点E为AB的中点,
∴∠ABC=60°,CE⊥AB,
∴AE=BE,
∴∠ECB=∠D=∠DEB=30°,
∴AE=DB,
故答案为:=;
(2) 在等边△ABC中,
∠ABC=∠ACB=∠BAC=60°,AB=BC=AC,
∵EF∥BC,
∴∠AEF=∠AFE=60°=∠BAC,
∴AE=AF=EF,
∴AB-AE=AC-AF,
即BE=CF,
∵∠ABC=∠EDB+∠BED=60°,
∠ACB=∠ECB+∠FCE=60°,
∵ED=EC,
∴∠EDB=∠ECB,
∵∠EBC=∠EDB+∠BED,∠ACB=∠ECB+∠FCE,
∴∠BED=∠FCE,
∴△DBE≌△EFC(SAS)
∴DB=EF,
∴AE=BD,
故答案为:=;
(3)CD的长是1或3.
参考做法如下:
当E在线段BA的延长线上,D在线段BC的延长线上时,如图1所示,
过E作EF⊥BD,垂足为F点,可得∠EFB=90°,
∵EC=ED,∴F为CD的中点,即CF=DF=![]() CD,
CD,
∵△ABC为等边三角形,∴∠ABC=60°,
∴∠BEF=30°,
∵BE=AB+AE=1+2=3,
∴FB=![]() EB=
EB=![]() ,
,
∴CF=FB-BC=![]() ,
,
则CD=2CF=1;
当E在线段AB的延长线上,D在线段CB的延长线上时,如图2所示,
过E作EF⊥BD,垂足为F点,可得∠EFC=90°,
∵EC=ED,∴F为CD的中点,即CF=DF=![]() CD,
CD,
∵△ABC为等边三角形,∴∠ABC=∠EBF=60°,
∴∠BEF=30°,
∵BE=AE-AB=2-1=1,
∴FB=![]() BE=
BE=![]() ,
,
∴CF=BC+FB=![]() ,
,
则CD=2CF=3,
综上,CD的值为1或3.
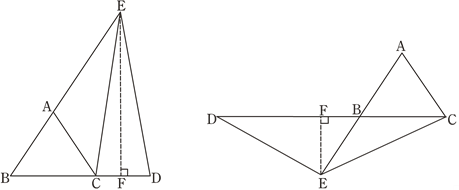
图1 图2
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,把三角形ABC向上平移3个单位长度,再向右平移2个单位长度,得到三角形A1B1C1.
(1)在图中画出三角形A1B1C1;
(2)写出点A1,B1的坐标;
(3)在y轴上是否存在一点P,使得三角形BCP与三角形ABC面积相等?若存在,请直接写出点P的坐标;若不存在,说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】小强、小亮、小文三位同学玩投硬币游戏.三人同时各投出一枚均匀硬币,若出现三个正面向上或三个反面向上,则小强赢;若出现2个正面向上一个反面向上,则小亮赢;若出现一个正面向上2个反面向上,则小文赢.下面说法正确的是( )
A.三人赢的概率都相等
B.小文赢的概率最小
C.小亮赢的概率最小
D.小强赢的概率最小 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在四边形ABCD中,AD∥BC,E为CD的中点,连接AE、BE,BE⊥AE,延长AE交BC的延长线于点F. 已知AD=2cm,BC=5cm.
(1)求证:FC=AD;
(2)求AB的长.
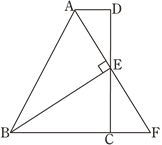
-
科目: 来源: 题型:
查看答案和解析>>【题目】推理填空:
如图所示,已知∠1 = ∠2,∠B = ∠C,可推得AB∥CD,

理由如下:
∵∠1 = ∠2(已知),且∠1 = ∠4(_____________________),
∴∠2 = ∠4(等量代换).
∴CE∥BF(__________________________).
∴∠_____= ∠3(________________________)
又∵∠B = ∠C(已知),
∴∠3= ∠B(等量代换),
∴AB∥CD(_____________________________).
-
科目: 来源: 题型:
查看答案和解析>>【题目】二次函数y=ax2+bx+c的图像如图所示,则反比例函数
 与一次函数y=bx+c在同一坐标系中的大致图像是( )
与一次函数y=bx+c在同一坐标系中的大致图像是( )
A.
B.
C.
D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知下面四个图形中,AB∥CD,探究四个图形中,∠APC与∠PAB,∠PCD的数量关系.
(1)图①中,∠APC与∠PAB,∠PCD的关系是__________________;
(2)图②中,∠APC与∠PAB,∠PCD的关系是__________________;
(3)请你在图③和图④中任选一个,说明∠APC与∠PAB,∠PCD的关系,并加以证明



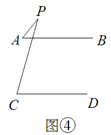
相关试题