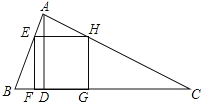
【题目】如图,△ABC为锐角三角形,AD是BC边上的高,正方形EFGH的一边FG在BC上,顶点E、H分别在AB、AC上,已知BC=40cm,AD=30cm.
(1)求证:△AEH∽△ABC;
(2)求这个正方形的边长与面积.
参考答案:
【答案】(1)证明见解析;(2)边长为![]() cm,面积为
cm,面积为![]() cm2.
cm2.
【解析】
试题分析:(1)根据EH∥BC即可证明.
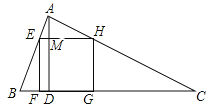
(2)如图设AD与EH交于点M,首先证明四边形EFDM是矩形,设正方形边长为x,再利用△AEH∽△ABC,得![]() ,列出方程即可解决问题.
,列出方程即可解决问题.
试题解析:(1)证明:∵四边形EFGH是正方形,∴EH∥BC,∴∠AEH=∠B,∠AHE=∠C,∴△AEH∽△ABC.
(2)解:如图设AD与EH交于点M.
∵∠EFD=∠FEM=∠FDM=90°,∴四边形EFDM是矩形,∴EF=DM,设正方形EFGH的边长为x,∵△AEH∽△ABC,∴![]() ,∴
,∴![]() ,∴x=
,∴x=![]() ,∴正方形EFGH的边长为
,∴正方形EFGH的边长为![]() cm,面积为
cm,面积为![]() cm2.
cm2.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在四边形ABCD中,AB∥CD,∠ABC=∠ADC,DE垂直于对角线AC,垂足是E,连接BE.
(1)求证:四边形ABCD是平行四边形;
(2)若点E是AC的中点,判断BE与AC的位置关系,并说明理由;
(3)若△ABE是等边三角形,AD=
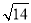 ,求对角线AC的长.
,求对角线AC的长.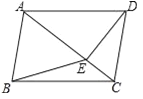
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB与CD相交于点O,∠A=∠AOC,∠B=∠BOD.
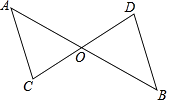
求证:∠C=∠D.
证明:∵∠A=∠AOC,∠B=∠BOD(已知)
又∠AOC=∠BOD()
∴∠A=∠B()
∴AC∥BD()
∴∠C=∠D() -
科目: 来源: 题型:
查看答案和解析>>【题目】计算:
(1)已知a+b=-3,ab=5,求多项式4a2b+4ab2-4a-4b的值;
(2)已知x2-3x-1=0,求代数式3-3 x2+9x的值?
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列命题是真命题的是( )
A.两边及其中一边的对角分别相等的两个三角形全等
B.平分弦的直径垂直于弦
C.一组对边平行且一组对角相等的四边形是平行四边形
D.两条直线被第三条直线所截,同位角相等
-
科目: 来源: 题型:
查看答案和解析>>【题目】关于x 的一元二次方程x2+2x-8=0的一个根为2,则它的另一个根为______.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下表是我市某一天在不同时段测得的气温情况
0:00
4:00
8:00
12:00
16:00
20:00
25℃
27℃
29℃
32℃
34℃
30℃
则这一天气温的极差是℃.
相关试题

