【题目】填写推理理由:
如图,CD∥EF,∠1=∠2,求证:∠3=∠ACB.
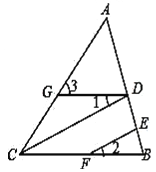
证明:∵CD∥EF,
∴∠DCB=∠2( ),
∵∠1=∠2,
∴∠DCB=∠1( ).
∴GD∥CB( ),
∴∠3=∠ACB( ).
参考答案:
【答案】 两直线平行,同位角相等;等量代换;内错角相等,两直线平行;两直线平行,同位角相等
【解析】试题分析:根据平行线的性质得出∠2=∠DCB,求出∠1=∠DCB,根据平行线的判定得出GD∥CB即可.
试题解析:如图,CD∥EF,∠1=∠2,求证:∠3=∠ACB.
证明:∵CD∥EF,
∴∠DCB=∠2(两直线平行,同位角相等)
∵∠1=∠2,
∴∠DCB=∠1.(等量代换)
∴GD∥CB(内错角相等,两直线平行).
∴∠3=∠ACB(两直线平行,同位角相等).
-
科目: 来源: 题型:
查看答案和解析>>【题目】工程建筑中经常采用三角形的结构,如屋顶钢架,其中的数学道理是_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列各组数中,以a,b,c为边长的三角形不是直角三角形的是( )
A. a=3,b=4,c=5B. a=4,b=5,c=6
C. a=6,b=8,c=10D. a=5,b=12,c=13
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知A(﹣2,a),B(1,b)是一次函数y=﹣2x+3的图象上的两个点,则a与b的大小关系是( )
A. a>bB. a<bC. a=bD. 不能确定
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在四边形ABCD中,AB=CD=6,AB⊥BC,AD⊥CD,∠BAD=60°,点M、N分别在AB、AD边上,若AM:MB=AN:ND=1:2,则tan∠MCN=( )
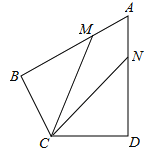
A、
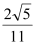 B、
B、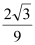 C、
C、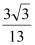 D、
D、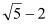
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,把一副三角板如图甲放置,其中∠ACB=DEC=90°,∠A=45°,∠D=30°,AB=6cm,DC=7cm.把三角板DCE绕点C顺时针旋转15°得到△D′CE′,如图乙,这时AB与CD′相交于点O,D′E′与AB、CB分别相交于点F、G,连接AD′.

(1)求∠OFE′的度数;
(2)求线段AD′的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】 阅读并补充下面推理过程:(1)
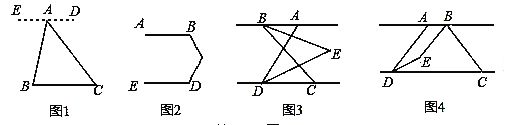
如图1,已知点A是BC外一点,连接AB,AC.
求∠BAC+∠B+∠C的度数.
解:过点A作ED∥BC,所以∠B= ,∠C= .
又因为∠EAB+∠BAC+∠DAC=180°.
所以∠B+∠BAC+∠C=180°.
方法运用:(2)如图2,已知AB∥ED,求∠B+∠BCD+∠D的度数.
深化拓展:(3)已知AB∥CD,点C在点D的右侧,∠ADC=70°,BE平分∠ABC,DE平分∠ADC,BE,DE所在的直线交于点E,点E在AB与CD两条平行线之间.
.如图3,点B在点A的左侧,若∠ABC=60°,则∠BED的度数为 °.
Ⅱ.如图4,点B在点A的右侧,且AB<CD,AD<BC.若∠ABC=n°,则∠BED的度数为 °.(用含n的代数式表示)
相关试题

