【题目】如果一个正整数能表示为两个连续偶数的平方差,那么称这个正整数就为“奇巧数,如![]() ,因此
,因此![]() 这三个数都是奇巧数。
这三个数都是奇巧数。
![]() 都是奇巧数吗?为什么?
都是奇巧数吗?为什么?
![]() 设这两个连续偶数为
设这两个连续偶数为![]() (其中
(其中![]() 为正整数),由这两个连续偶数构造的奇巧数是
为正整数),由这两个连续偶数构造的奇巧数是![]() 的倍数吗?为什么?
的倍数吗?为什么?
![]() 研究发现:任意两个连续“奇巧数”之差是同一个数,请给出验证。
研究发现:任意两个连续“奇巧数”之差是同一个数,请给出验证。
参考答案:
【答案】(1)52是奇巧数,72不是奇巧数;(2)不是8的倍数,理由见解析;(3)见解析.
【解析】
(1)判断52与72是否能写成两个连续偶数的平方差即可;
(2)先计算2n+2与2n的平方差,再进行判断即可;
(3)取四个连续的偶数2n,2n+2,2n+4,2n+6(n为正整数),可得三个连续的奇巧数,再作差比较即得结果.
解:(1)![]() ,
,![]() ,因为52是两个连续偶数的平方差,所以52是奇巧数,而72是两个连续奇数的平方差,不是两个连续偶数的平方差,所以72不是奇巧数;
,因为52是两个连续偶数的平方差,所以52是奇巧数,而72是两个连续奇数的平方差,不是两个连续偶数的平方差,所以72不是奇巧数;
(2)由2n,2n+2构造的奇巧数不是8的倍数,理由如下:
![]() ,
,
因为n为正整数,所以2n+1是奇数,所以奇巧数4(2n+1)是4的倍数,不是8的倍数;
(3)验证:12,20与20,28都是连续的奇巧数,它们的差都是8,是同一个数.
一般的,设四个连续的偶数为:2n,2n+2,2n+4,2n+6(n为正整数),则
![]() ,
,
![]() ,
,
![]() ,
,
所以8n+4,8n+12,8n+20是三个连续的奇巧数,
且![]() ,
,![]() ,
,
所以任意两个连续“奇巧数”之差是同一个数,这个数是8.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图所示,在△ABC中,∠B=90°,AB=5cm,BC=7cm,点P从点A开始沿AB边向点B以1cm/s的速度移动,点Q从点B开始沿BC边向点C以2cm/s的速度移动.
(1)如果P,Q分别从A,B同时出发,那么几秒后,△PBQ的面积等于4cm2?
(2)如果P,Q分别从A,B同时出发,那么几秒后,△PBQ中PQ的长度等于5cm?
(3)在(1)中,当P,Q出发几秒时,△PBQ有最大面积?
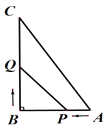
-
科目: 来源: 题型:
查看答案和解析>>【题目】在一次中学生田径运动会上,根据参加男子跳高初赛的运动员的成绩(单位:m),绘制出如下的统计图①和图②,请根据相关信息,解答下列问题:

(Ⅰ)图1中a的值为 ;
(Ⅱ)求统计的这组初赛成绩数据的平均数、众数和中位数;
(Ⅲ)根据这组初赛成绩,由高到低确定9人进入复赛,请直接写出初赛成绩为1.65m的运动员能否进入复赛.
-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读下列解题过程:
计算:(-5)÷
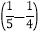 ×20.
×20.解:原式=(-5)÷
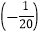 ×20 (第一步)
×20 (第一步)=(-5)÷(-1) (第二步)
=-5. (第三步)
(1)上述解题过程中有两处错误:
第一处是第________步,错误的原因是__________________________;
第二处是第________步,错误的原因是_______________________.
(2)把正确的解题过程写出来.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,横、纵坐标均为整数的点叫做整数点,设坐标轴的单位长度为1cm,整数点P从原点O出发,速度为1cm/s,且点P只能向上或向右运动,请回答下列问题:
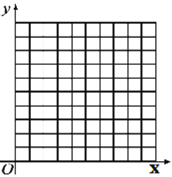
(1)填表:
点P从O点出发的时间
可以到达的整坐标
可以到达整数点的个数
1秒
(0,1),(1,0)
2
2秒
(0,2),(2,0),(1,1)
3
3秒
( )
( )
(2)当点P从点O出发10秒,可到达的整数点的个数是____________个;
(3)当点P从O点出发____________秒时,可得到整数点(10,5).
-
科目: 来源: 题型:
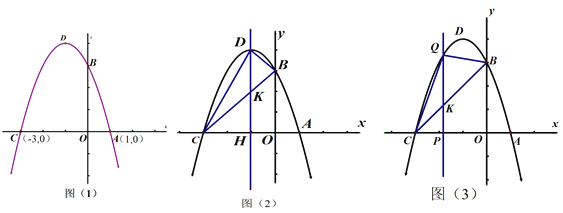
查看答案和解析>>【题目】已知,如图,抛物线与x轴交点坐标为A(1,0),C(-3,0),
(1)若已知顶点坐标D为(-1,4)或B点(0,3),选择适当方式求抛物线的解析式.
(2)若直线DH为抛物线的对称轴,在(1)的基础上,求线段DK的长度,并求△DBC的面积.
(3)将图(2)中的对称轴向左移动,交x轴于点p(m,0)(-3<m<-1),与线段BC、抛物线的交点分别为点K、Q,用含m的代数式表示QK的长度,并求出当m为何值时,△BCQ的面积最大?
-
科目: 来源: 题型:
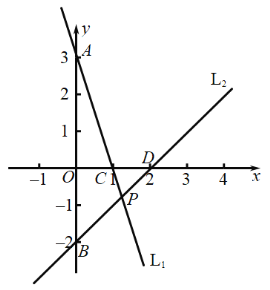
查看答案和解析>>【题目】如图,L1、L2分别表示两个一次函数的图象,它们相交于点P.
(1)求出两条直线的函数关系式;
(2)点P的坐标可看作是哪个二元一次方程组的解?
(3)求出图中△APB的面积.
相关试题

