【题目】如图,在△ABC中,AB=AC=11,∠BAC=120°,AD是△ABC的中线,AE是∠BAD的角平分线,DF∥AB交AE的延长线于点E,则DF的长为( )
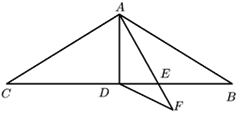
A. 4.5 B. 5 C. 5.5 D. 6
参考答案:
【答案】C
【解析】
根据等腰三角形三线合一的性质可得AD⊥BC,∠BAD=∠CAD,再求出∠DAE=∠EAB=30°,然后根据平行线的性质求出∠F=∠BAE=30°,从而得到∠DAE=∠F,再根据等角对等边求出AD=DF,然后求出∠B=30°,根据直角三角形30°角所对的直角边等于斜边的一半解答.
解:∵AB=AC,AD是△ABC的中线,
∴AD⊥BC,∠BAD=∠CAD=![]() ∠BAC=
∠BAC=![]() ×120°=60°,
×120°=60°,
∵AE是∠BAD的角平分线,
∴∠DAE=∠EAB=![]() ∠BAD=
∠BAD=![]() ×60°=30°,
×60°=30°,
∵DF∥AB,
∴∠F=∠BAE=30°,
∴∠DAE=∠F=30°,
∴AD=DF,
∵∠B=90°-60°=30°,
∴AD=![]() AB=
AB=![]() ×11=5.5,
×11=5.5,
∴DF=5.5.
故选:C.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在直线AB上任取一点O,过点O作射线OC、OD,使∠COD=100°,当∠AOC=30°时,∠BOD的度数是( )
A. 50° B. 80° C. 80°或150° D. 50°或110°
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC中,∠ABC、∠ACB的平分线相交于O,MN过点O且与BC平行.△ABC的周长为20,△AMN的周长为12,则BC的长为( )
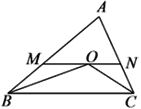
A. 10 B. 16 C. 8 D. 4
-
科目: 来源: 题型:
查看答案和解析>>【题目】某商场用2700元购进甲、乙两种商品共100件,这两种商品的进价、标价如下表所示:

(1)求购进两种商品各多少件?
(2)商品将两种商品全部卖出后,获得的利润是多少元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算:(
 )﹣1+2cos45°+|
)﹣1+2cos45°+|  ﹣1|﹣(3.14﹣π)0 .
﹣1|﹣(3.14﹣π)0 . -
科目: 来源: 题型:
查看答案和解析>>【题目】解不等式3(x﹣1)≤
 ,并把它的解集在数轴上表示出来.
,并把它的解集在数轴上表示出来. 
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,等边三角形ABC的边长为4,AD是BC边上的中线,F是AD边上的动点,E是AC边上一点.若AE=2,当EF+CF取得最小值时,∠ECF的度数为( )

A. 20° B. 25° C. 30° D. 45°
相关试题

