【题目】如图,在△ABC中,两条中线BE、CD相交于点O,则S△ADE:S△COE= . 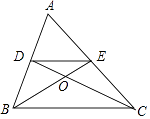
参考答案:
【答案】2:1
【解析】解:∵在△ABC中,两条中线BE、CD相交于点O,
∴DE为中位线,
∴DE∥BC,DE= ![]() BC,
BC,
∴△ADE∽△ABC,△DOE∽△COB,
∴S△ADE:S△ABC=1:4,S△DOE:S△COB=1:4,
∵OD:OC=1:2,
∴S△DOE:S△COE=1:2,S△DOB:S△COB=1:2,
∴S△COE= ![]() S四边形DBCE,
S四边形DBCE,
则S△ADE:S△COE=2:1.
所以答案是:2:1
【考点精析】解答此题的关键在于理解三角形中位线定理的相关知识,掌握连接三角形两边中点的线段叫做三角形的中位线;三角形中位线定理:三角形的中位线平行于三角形的第三边,且等于第三边的一半,以及对相似三角形的判定与性质的理解,了解相似三角形的一切对应线段(对应高、对应中线、对应角平分线、外接圆半径、内切圆半径等)的比等于相似比;相似三角形周长的比等于相似比;相似三角形面积的比等于相似比的平方.
-
科目: 来源: 题型:
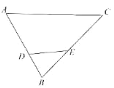
查看答案和解析>>【题目】尺规作图(不用写出作法,保留作图痕迹):
(1)在 DE 的上方,求作
 FDE,使得
FDE,使得 FDE≌
FDE≌ BDE;
BDE; (2)若∠B=50°,则∠ADF+∠CEF= °.
-
科目: 来源: 题型:
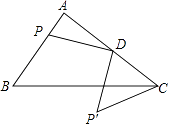
查看答案和解析>>【题目】如图,在Rt△ABC中,∠A=90°,AB=3,AC=4,D为AC中点,P为AB上的动点,将P绕点D逆时针旋转90°得到P′,连CP′,则线段CP′的最小值为 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在
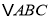 中,
中,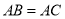 ,点
,点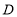 是
是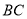 边上的中点,
边上的中点,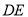 、
、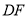 分别垂直
分别垂直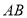 、
、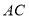 于点
于点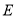 和
和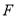 .求证:
.求证: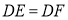
-
科目: 来源: 题型:
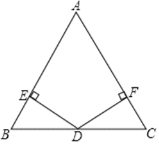
查看答案和解析>>【题目】如图,在矩形ABCD中,AD=10,E为AB上一点,且AE=
 AB=a,连结DE,F是DE中点,连结BF,以BF为直径作⊙O.
AB=a,连结DE,F是DE中点,连结BF,以BF为直径作⊙O.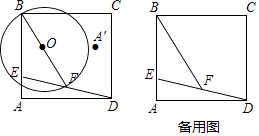
(1)用a的代数式表示DE2= , BF2=;
(2)求证:⊙O必过BC的中点;
(3)若⊙O与矩形ABCD各边所在的直线相切时,求a的值;
(4)作A关于直线BF的对称点A′,若A′落在矩形ABCD内部(不包括边界),则a的取值范围 . (直接写出答案) -
科目: 来源: 题型:
查看答案和解析>>【题目】已知△ABC中,∠BAC=90°,AB=AC.
(1)如图,D为AC上任一点,连接BD,过A点作BD的垂线交过C点与AB平行的直线CE于点E.求证:BD=AE.
(2)若点D在AC的延长线上,如图,其他条件同(1),请画出此时的图形,并猜想BD与AE是否仍然相等?说明你的理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,抛物线y=ax2+3x交x轴正半轴于点A(6,0),顶点为M,对称轴MB交x轴于点B,过点C(2,0)作射线CD交MB于点D(D在x轴上方),OE∥CD交MB于点E,EF∥x轴交CD于点F,作直线MF.
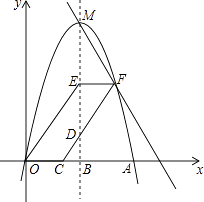
(1)求a的值及M的坐标;
(2)当BD为何值时,点F恰好落在该抛物线上?
(3)当∠DCB=45°时:
①求直线MF的解析式;
②延长OE交FM于点G,四边形DEGF和四边形OEDC的面积分别记为S1、S2 , 则S1:S2的值为(直接写答案)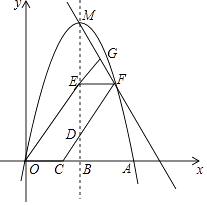
相关试题

