【题目】如图,抛物线y=ax2+3x交x轴正半轴于点A(6,0),顶点为M,对称轴MB交x轴于点B,过点C(2,0)作射线CD交MB于点D(D在x轴上方),OE∥CD交MB于点E,EF∥x轴交CD于点F,作直线MF.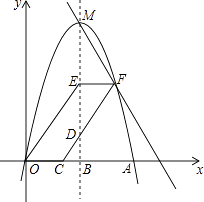
(1)求a的值及M的坐标;
(2)当BD为何值时,点F恰好落在该抛物线上?
(3)当∠DCB=45°时:
①求直线MF的解析式;
②延长OE交FM于点G,四边形DEGF和四边形OEDC的面积分别记为S1、S2 , 则S1:S2的值为(直接写答案)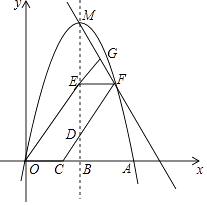
参考答案:
【答案】
(1)解:把A(6,0)代入y=ax2+3x得36a+18=0,解得a=﹣ ![]() ;
;
抛物线解析式为y=﹣ ![]() x2+3x,
x2+3x,
∵y=﹣ ![]() (x﹣3)2+
(x﹣3)2+ ![]() ,
,
∴M点的坐标为(3, ![]() )
)
(2)解:∵CF∥OE,EF∥OC,
∴四边形OCFE为平行四边形,
∴EF=OC=2,
∵抛物线的对称轴为直线x=3,B(3,0),
∴F点的横坐标为5,
当x=5时,y=﹣ ![]() x2+3x=
x2+3x= ![]() ,即F(5,
,即F(5, ![]() ),
),
∴BE= ![]() ,
,
∵EF∥BC,
∴△BCD∽△EFD,
∴ ![]() =
= ![]() =
= ![]() ,
,
∴BD= ![]() BE=
BE= ![]() ×
× ![]() =
= ![]() ,
,
即当BD为 ![]() 时,点F恰好落在该抛物线上
时,点F恰好落在该抛物线上
(3)∵CD∥OE,∴∠BOE=∠DCB=45°∴△BOE为等腰直角三角形, ∴BE=OE=3,则E(3,3),∴直线OE的解析式为y=x,同理可得△BCD为等腰直角三角形,∴BD=BC=1,∴DE=2,∵EF∥OC,EF=OC=2,∴F(5,3),设直线MF的解析式为y=kx+b,把M(3,![]() ),F(5,3)代入得
),F(5,3)代入得  ,解得
,解得  ,∴直线MF的解析式为y=﹣
,∴直线MF的解析式为y=﹣ ![]() x+
x+ ![]() ;,
;,![]()
【解析】解:(3)②解方程组  得
得  ,则G(
,则G( ![]() ,
, ![]() ),
),
∴S1=S△GEF+S△DEF= ![]() ×2×(
×2×( ![]() ﹣3)+
﹣3)+ ![]() ×2×2=
×2×2= ![]() ,
,
S2=S△BOE﹣S△BCD= ![]() ×3×3﹣
×3×3﹣ ![]() ×1×1=4,
×1×1=4,
∴ ![]() =
= ![]() =
= ![]() .
.
所以答案是 ![]() .
.
【考点精析】本题主要考查了确定一次函数的表达式和二次函数的最值的相关知识点,需要掌握确定一个一次函数,需要确定一次函数定义式y=kx+b(k不等于0)中的常数k和b.解这类问题的一般方法是待定系数法;如果自变量的取值范围是全体实数,那么函数在顶点处取得最大值(或最小值),即当x=-b/2a时,y最值=(4ac-b2)/4a才能正确解答此题.
-
科目: 来源: 题型:
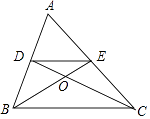
查看答案和解析>>【题目】如图,在△ABC中,两条中线BE、CD相交于点O,则S△ADE:S△COE= .
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在矩形ABCD中,AD=10,E为AB上一点,且AE=
 AB=a,连结DE,F是DE中点,连结BF,以BF为直径作⊙O.
AB=a,连结DE,F是DE中点,连结BF,以BF为直径作⊙O.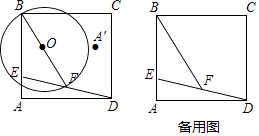
(1)用a的代数式表示DE2= , BF2=;
(2)求证:⊙O必过BC的中点;
(3)若⊙O与矩形ABCD各边所在的直线相切时,求a的值;
(4)作A关于直线BF的对称点A′,若A′落在矩形ABCD内部(不包括边界),则a的取值范围 . (直接写出答案) -
科目: 来源: 题型:
查看答案和解析>>【题目】已知△ABC中,∠BAC=90°,AB=AC.
(1)如图,D为AC上任一点,连接BD,过A点作BD的垂线交过C点与AB平行的直线CE于点E.求证:BD=AE.
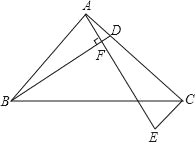
(2)若点D在AC的延长线上,如图,其他条件同(1),请画出此时的图形,并猜想BD与AE是否仍然相等?说明你的理由.
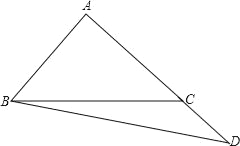
-
科目: 来源: 题型:
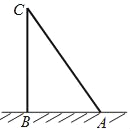
查看答案和解析>>【题目】《九章算术》是中国传统数学最重要的著作,奠定了中国传统数学的基本框架.其中记载了一个“折竹抵地”问题:“今有竹高二丈,末折抵地,去本六尺,问折者高几何?”
译文:“有一根竹子,原高二丈(1丈=10尺),现被风折断,竹梢触地面处与竹根的距离为6尺,问折断处离地面的高度为多少尺?”
如图,我们用点A,B,C分别表示竹梢,竹根和折断处,设折断处离地面的高度BC=x尺,则可列方程为_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】温州某学校搬迁,教师和学生的寝室数量在增加,若该校今年准备建造三类不同的寝室,分别为单人间(供一个人住宿),双人间(供两个人住宿),四人间(供四个人住宿).因实际需要,单人间的数量在20至于30之间(包括20和30),且四人间的数量是双人间的5倍.
(1)若2015年学校寝室数为64个,2017年建成后寝室数为121个,求2015至2017年的平均增长率;
(2)若建成后的寝室可供600人住宿,求单人间的数量;
(3)若该校今年建造三类不同的寝室的总数为180个,则该校的寝室建成后最多可供多少师生住宿? -
科目: 来源: 题型:
查看答案和解析>>【题目】下面是小芸设计的“作三角形一边上的高”的尺规作图过程.
已知:△ABC.
求作:△ABC的边BC上的高AD.
作法:①以点A为圆心,适当长为半径画弧,
交直线BC于点M,N;
②分别以点M,N为圆心,以大于
 MN的长为半径画弧,两弧相交于点P;
MN的长为半径画弧,两弧相交于点P;③作直线AP交BC于点D,则线段AD即为所求△ABC的边BC上的高.
根据小芸设计的尺规作图过程,
(1)使用直尺和圆规,补全图形;(保留作图痕迹)
(2)完成下面的证明:
证明:∵AM= ,MP= ,
∴AP是线段MN的垂直平分线.( )(填推理的依据)
∴AD⊥BC于D,即线段AD为△ABC的边BC上的高.

相关试题

