【题目】如图,在矩形ABCD中,AD=10,E为AB上一点,且AE= ![]() AB=a,连结DE,F是DE中点,连结BF,以BF为直径作⊙O.
AB=a,连结DE,F是DE中点,连结BF,以BF为直径作⊙O.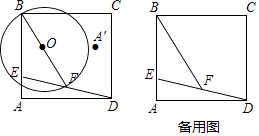
(1)用a的代数式表示DE2= , BF2=;
(2)求证:⊙O必过BC的中点;
(3)若⊙O与矩形ABCD各边所在的直线相切时,求a的值;
(4)作A关于直线BF的对称点A′,若A′落在矩形ABCD内部(不包括边界),则a的取值范围 . (直接写出答案)
参考答案:
【答案】
(1)a2+100,![]()
(2)证明:如图1,设⊙O交BC于H,连接FH,
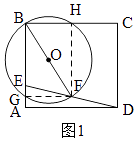
∵BF是⊙O的直径,
∴∠BHF=90°,
∴∠ABC=∠BHF=∠AGF=90°,
∴四边形BGFH是矩形,
∴BH=GF= ![]() AD=
AD= ![]() BC,
BC,
∴H是BC的中点,
即:⊙O必过BC的中点
(3)解:分两种情况:
①如图2,当⊙O与边CD相切时,设切点为M,连接OM、FH交于N,则OM⊥CD,
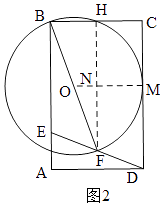
∴OM=ON+MN= ![]() +5=
+5= ![]() ,
,
∵OM⊥FH,
∴NF= ![]() FH=
FH= ![]() ×
× ![]() =
= ![]() a,
a,
Rt△ONF中,ON2+NF2=OF2=OM2,
∴ ![]() +(
+( ![]() )2=
)2= ![]() ,
,
a= ![]() ,
,
∵a>0,
∴a= ![]() ,
,
②如图3,当⊙O与边AD相切时,设切点为Q,
连接OQ,则OQ⊥AD,连接FG,交OQ于P,
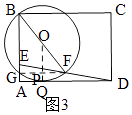
∴OQ=OP+PQ= ![]() BG+AG=
BG+AG= ![]() +
+ ![]() =
= ![]() a,
a,
由(1)知: ![]() 且BF=2OQ,
且BF=2OQ,
∴25+ ![]() a2=(2×
a2=(2× ![]() a)2,
a)2,
a= ![]() ,
,
综上所述,若⊙O与矩形ABCD各边所在的直线相切时,a的值为 ![]() 或
或 ![]()
(4)![]() <a<
<a< ![]()
【解析】解:(1)如图1,∵四边形ABCD是矩形,
∴∠A=90°,
在Rt△AED中,AE=a,AD=10,
由勾股定理得:ED2=AE2+AD2=a2+102=a2+100,
设⊙O交AB于G,连接FG,
∵BF是⊙O的直径,
∴∠BGF=90°,
∵∠A=90°,
∴∠BGF=∠A,
∴FG∥AD,
∵F是ED的中点,
∴GF= ![]() AD=5,EG=AG=
AD=5,EG=AG= ![]() a,
a,
∵AE= ![]() AB=a,
AB=a,
∴AB=4a,
∴BG=4a﹣ ![]() a=
a= ![]() a,
a,
由勾股定理得:BF2=BG2+GF2,
∴BF2= ![]() +52=
+52= ![]() +25=
+25= ![]() ,
,
所以答案是:a2+100; ![]() ;
;
⑷如图4,当A的对称点A′恰好在边BD上时,连接AA′交BF于H,连接AF、A′F,过F作MN⊥BC,交BC于M,交AD于N,则MN⊥AD,
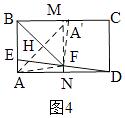
∵A关于直线BF的对称点A′,
∴BF是AA′的垂直平分线,
∴AF=A′F,AB=A′B=4a,
由(1)(2)得:FN= ![]() a,FM=
a,FM= ![]() a,A′M=4a﹣5,AN=5,
a,A′M=4a﹣5,AN=5,
由勾股定理得: ![]() =(4a﹣5)2+
=(4a﹣5)2+ ![]() ,
,
解得:a1=0(舍),a2= ![]() ,
,
∴当a< ![]() 时,A′落在矩形ABCD外部(包括边界),
时,A′落在矩形ABCD外部(包括边界),
如图5,当A′落在边CD上时,连接AA′、A′B,过F作MG⊥AB,则MG⊥CD,
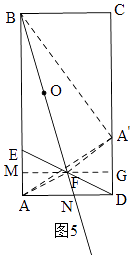
设射线BF交AD于N,
易得A′G=AM=DG= ![]() a,A′C=3a,
a,A′C=3a,
∵BF是AA′的垂直平分线,
∴AB=A′B,
则(4a)2=102+(3a)2,
a= ![]() ,
,
∴a的取值范围是: ![]() <a<
<a< ![]() ,
,
所以答案是: ![]() <a<
<a< ![]() .
.
【考点精析】根据题目的已知条件,利用线段垂直平分线的性质和勾股定理的概念的相关知识可以得到问题的答案,需要掌握垂直于一条线段并且平分这条线段的直线是这条线段的垂直平分线;线段垂直平分线的性质定理:线段垂直平分线上的点和这条线段两个端点的距离相等;直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△ABC中,∠A=90°,AB=3,AC=4,D为AC中点,P为AB上的动点,将P绕点D逆时针旋转90°得到P′,连CP′,则线段CP′的最小值为 .
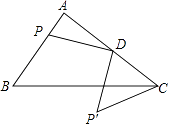
-
科目: 来源: 题型:
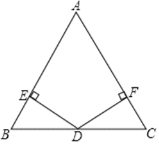
查看答案和解析>>【题目】如图,在
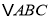 中,
中,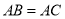 ,点
,点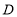 是
是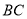 边上的中点,
边上的中点,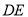 、
、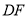 分别垂直
分别垂直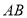 、
、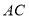 于点
于点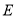 和
和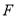 .求证:
.求证: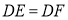
-
科目: 来源: 题型:
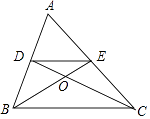
查看答案和解析>>【题目】如图,在△ABC中,两条中线BE、CD相交于点O,则S△ADE:S△COE= .
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知△ABC中,∠BAC=90°,AB=AC.
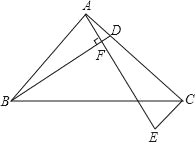
(1)如图,D为AC上任一点,连接BD,过A点作BD的垂线交过C点与AB平行的直线CE于点E.求证:BD=AE.
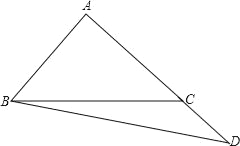
(2)若点D在AC的延长线上,如图,其他条件同(1),请画出此时的图形,并猜想BD与AE是否仍然相等?说明你的理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,抛物线y=ax2+3x交x轴正半轴于点A(6,0),顶点为M,对称轴MB交x轴于点B,过点C(2,0)作射线CD交MB于点D(D在x轴上方),OE∥CD交MB于点E,EF∥x轴交CD于点F,作直线MF.
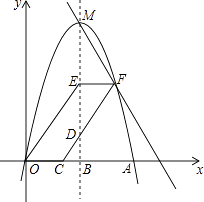
(1)求a的值及M的坐标;
(2)当BD为何值时,点F恰好落在该抛物线上?
(3)当∠DCB=45°时:
①求直线MF的解析式;
②延长OE交FM于点G,四边形DEGF和四边形OEDC的面积分别记为S1、S2 , 则S1:S2的值为(直接写答案)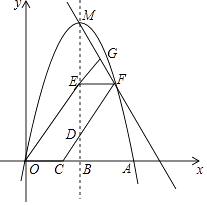
-
科目: 来源: 题型:
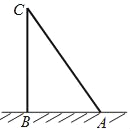
查看答案和解析>>【题目】《九章算术》是中国传统数学最重要的著作,奠定了中国传统数学的基本框架.其中记载了一个“折竹抵地”问题:“今有竹高二丈,末折抵地,去本六尺,问折者高几何?”
译文:“有一根竹子,原高二丈(1丈=10尺),现被风折断,竹梢触地面处与竹根的距离为6尺,问折断处离地面的高度为多少尺?”
如图,我们用点A,B,C分别表示竹梢,竹根和折断处,设折断处离地面的高度BC=x尺,则可列方程为_____.
相关试题

