【题目】如图,△ABC中,∠BAC=60°,∠ABC、∠ACB的平分线交于E,D是AE延长线上一点,且∠BDC=120°.下列结论:①∠BEC=120°;②DB=DC;③DB=DE;④∠BDE=∠BCA.其中正确结论的个数为( )
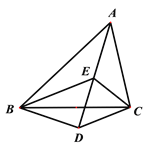
A. 1 B. 2 C. 3 D. 4
参考答案:
【答案】D
【解析】分析:根据三角形内角和等于180°求出∠ABC+∠ACB,再根据角平分线的定义求出∠EBC+∠ECB,然后求出∠BEC=120°,判断①正确;过点D作DF⊥AB于F,DG⊥AC的延长线于G,根据角平分线上的点到角的两边的距离相等可得DF=DG,再求出∠BDF=∠CDG,然后利用“角边角”证明△BDF和△CDG全等,根据全等三角形对应边相等可得BD=CD,得出②正确;再根据等边对等角求出∠DBC=30°,然后根据三角形的一个外角等于与它不相邻的两个内角的和以及角平分线的定义求出∠DBE=∠DEB,根据等角对等边可得BD=DE,判断③正确;再求出B,C,E三点在以D为圆心,以BD为半径的圆上,根据同弧所对的圆周角等于圆心角的一半可得∠BDE=2∠BCE=∠BCA,判断④正确.
详解:∵∠BAC=60°, ∴∠ABC+∠ACB=180°-60°=120°,
∵BE、CE分别为∠ABC、∠ACB的平分线, ∴∠EBC=![]() ∠ABC,∠ECB=
∠ABC,∠ECB=![]() ∠ACB,
∠ACB,
∴∠EBC+∠ECB=![]() (∠ABC+∠ACB)=
(∠ABC+∠ACB)=![]() ×120°=60°,
×120°=60°,
∴∠BEC=180°-(∠EBC+∠ECB)=180°-60°=120°,故①正确;
如图,过点D作DF⊥AB于F,DG⊥AC的延长线于G,
∵BE、CE分别为∠ABC、∠ACB的平分线, ∴AD为∠BAC的平分线,
∴DF=DG, ∴∠FDG=360°-90°×2-60°=120°, 又∵∠BDC=120°,
∴∠BDF+∠CDF=120°,∠CDG+∠CDF=120°, ∴∠BDF=∠CDG,
∴△BDF≌△CDG(ASA), ∴DB=CD,故②正确;
∴∠DBC=![]() (180°-120°)=30°, ∴∠DBE=∠DBC+∠CBE=30°+∠CBE,
(180°-120°)=30°, ∴∠DBE=∠DBC+∠CBE=30°+∠CBE,
∵BE平分∠ABC,AE平分∠BAC, ∴∠ABE=∠CBE,∠BAE=![]() ∠BAC=30°,
∠BAC=30°,
根据三角形的外角性质,∠DEB=∠ABE+∠BAE=∠ABE+30°,∴∠DBE=∠DEB,
∴DB=DE,故③正确;
∵DB=DE=DC, ∴B,C,E三点在以D为圆心,以BD为半径的圆上,
∴∠BDE=2∠BCE=∠BCA,故④正确;故选D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】观察下列等式:
12×231=132×21,
13×341=143×31,
23×352=253×32,
34×473=374×43,
62×286=682×26,
……
以上每个等式中两边数字是分别对称的,且每个等式中组成两位数与三位数的数字之间具有相同规律,我们称这类等式为“数字对称等式”.
(1)根据上述各式反映的规律填空,使式子成为“数字对称等式”:
①52× = ×25;
② ×396=693× .
(2)设这类等式左边两位数的十位数字为
 ,个位数字为
,个位数字为 ,且2≤
,且2≤ ≤9,写出表示“数字对称等式”一般规律的式子(含
≤9,写出表示“数字对称等式”一般规律的式子(含 、
、 ),并说明理由.
),并说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】为了打造区域中心城市,实现攀枝花跨越式发展,我市花城新区建设正按投资计划有序推进.花城新区建设工程部,因道路建设需要开挖土石方,计划每小时挖掘土石方540m3,现决定向某大型机械租赁公司租用甲、乙两种型号的挖掘机来完成这项工作,租赁公司提供的挖掘机有关信息如表:

(1)若租用甲、乙两种型号的挖掘机共8台,恰好完成每小时的挖掘量,则甲、乙两种型号的挖掘机各需多少台?
(2)请你设计一种方案,不仅每小时支付的租金最少,又恰好能完成每小时的挖掘量?
-
科目: 来源: 题型:
查看答案和解析>>【题目】你会求
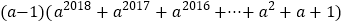 的值吗?这个问题看上去很复杂,我们可以先考虑简单的情况,通过计算,探索规律:
的值吗?这个问题看上去很复杂,我们可以先考虑简单的情况,通过计算,探索规律: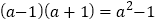
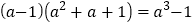
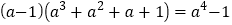
(1)由上面的规律我们可以大胆猜想,得到
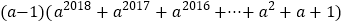 =________
=________ 利用上面的结论,求
(2)
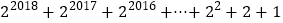 的值;
的值;(3)求
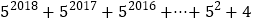 的值.
的值. -
科目: 来源: 题型:
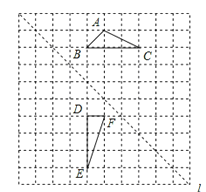
查看答案和解析>>【题目】如图,在边长为1个单位长度的小正方形组成的网格中,给出了格点△ABC和△DEF(顶点为网格线的交点),以及过格点的直线l.
①将△ABC向右平移两个单位长度,再向下平移两个单位长度,画出平移后的三角形△A’B’C’;
②画出△DEF关于直线l对称的三角形△D’E’F’;
③填空:∠C+∠E= .
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知关于x,y的方程组
 的解满足x<0,y>0.
的解满足x<0,y>0.(1)x=________, y=________(用含a的代数式表示);
(2)求a的取值范围;
(3)若2x8y=2m,用含有a的代数式表示m,并求m的取值范围.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某地区为绿化环境,计划购买甲、乙两种树苗共计n棵.有关甲、乙两种树苗的信息如图所示:

(1)当n=400时,如果购买甲、乙两种树苗共用27000元,那么甲、乙两种树苗各买了多少棵?
(2)实际购买这两种树苗的总费用恰好为27000元,其中甲种树苗买了m棵.
①写出m与n满足的关系式;
②要使这批树苗的成活率不低于92%,求n的最大值.
相关试题

